Anti-PISA
Anatoly Krasnyansky: Errors in PISA tasks
Содержание раздела
1. Фрагмент пизовской задачи "Ультразвук".
2. Приложение № 1. Физические принципы ульразвукового метода исследования.
3. Приложение № 2 Равномерное и равноускоренное прямолинейное движение. Равномерное и равноускоренное прямолинейное движение.
4. Приложение № 3. Равноускоренное движение. Задачи.
Фрагмент пизовской задачи "Ультразвук"
Составители задачи международной программы PISA-2006 в качестве правильного приняли следующий ответ: Расстояние = скорость/время и объяснили: "Хотя формула неверная, учащийся правильно указал, что нужно измерить «время»"
Подробнее: смотрите задачу "Ультразвук" международной программы PISA-2006.
———————————————————————-
Источник информации о задачах программы PISA: http://www.centeroko.ru/public.htm
РОССИЙСКАЯ АКАДЕМИЯ ОБРАЗОВАНИЯ
ИНСТИТУТ СОДЕРЖАНИЯ И МЕТОДОВ ОБУЧЕНИЯ
ЦЕНТР ОЦЕНКИ КАЧЕСТВА ОБРАЗОВАНИЯ
ПРИМЕРЫ ЗАДАНИЙ ПО ЕСТЕСТВОЗНАНИЮ
Международная оценка образовательных достижений учащихся
(Programme for International Student Assessment – PISA)
У ч и м с я
д л я ж и з н и !
Москва, 2007
СОСТАВИТЕЛИ: КОВАЛЕВА Г.С., к.п.н., КОШЕЛЕНКО Н.Г.
ОФОРМЛЕНИЕ: БАРАНОВА В.Ю.
Задача "Ультразвук"
Вопрос № 1
Чтобы создать изображение плода ультразвуковой аппарат должен вычислить расстояние между плодом и датчиком. Ультразвуковые волны распространяются в брюшной полости со скоростью 1540 м/с. Что должен измерить ультразвуковой аппарат, чтобы вычислить расстояние между плодом и детектором.
ОЦЕНКА ВЫПОЛНЕНИЯ ЗАДАНИЯ
Ответ принимается полностью – 1 балл.
Процент российских учащихся, набравших данный балл 35,3
Код 1: Надо измерить время, в течение которого ультразвуковая волна проходит от датчика до поверхности плода и обратно.
• Время прохождения волны.
• Время.
• Время. Расстояние = скорость/время (Хотя формула неверная, учащийся правильно указал, что нужно измерить «время».) — "Правильный" ответ выделил жирным шрифтом А.В. Краснянский.
• Нужно определить когда ультразвук достигнет плода.
Ответ не принимается
Код 0: Другие ответы.
• Расстояние.
Код 9: Ответ отсутствует.
Контекст: личностный
Тип вопроса: с открытым свободно-конструируемым ответом
Компетенция: научное объяснение явлений ("Компетенцию" жирным шрифтом выделил А.В. Краснянский)
Содержание: физические системы
Область применения: связь естествознания и технологии
Комментарий Анатолия Краснянского
Эта задача, по мнению составителей, проверяет способность ("компетенцию") учащихся научно объяснять явления. Вот так: школьник ничего не знает о свойствах ультразвука и особенностях его распространения в неоднородных средах, не знает ЭЛЕМЕНТАРНУЮ формулу и при этом научно объясняет явление!
И ЭТОТ ВЗДОР НАМ ВПИХИВАЮТ КАК ДОСТИЖЕНИЕ ПЕДАГОГИЧЕСКОЙ НАУКИ!
1. Анализ условия задачи
Анализ высказывания: "Чтобы создать изображение плода ультразвуковой аппарат должен вычислить расстояние между плодом и датчиком". Здесь неясно, что означает "расстояние между плодом и датчиком". Об расстоянии между плодом и датчиком можно говорить только в том случае, когда размеры плода и датчика намного меньше, чем это расстояние. Правильно: "Чтобы создать изображение плода ультразвуковой аппарат должен вычислить расстояния (множество расстояний) между датчиком и поверхностью плода (раздела границы двух сред: околоплодная жидкость — тело ребенка) при различных положениях датчика.
2. Обоснованный ответ на задачу
Чтобы рассчитать время, в течение которого ультразвуковая волна проходит от датчика до поверхности плода и обратно, необходимо сделать следующие предположения:
1. Ультразвуковые волны распространяются прямолинейно.
2. Волны движутся с постоянной скоростью.
3. Датчик регистрирует только волны, отраженные на 180о от границы двух сред (околоплодная жидкость — тело ребенка)
Для определения расстояния по известной скорости используем формулу 2S = vt, где S — расстояние от датчика до поверхности плода, от которой отражается ультразвуковая волна, v — скорость ульразвуковой волны; S = vt/2 . Поскольку скорость волн известна, датчик должен измерить промежуток времени t между испусканием ультразвуковой волны и приемом отраженной волны.
Очевидно, что код 1 ("Надо измерить время, в течение которого ультразвуковая волна проходит от датчика до поверхности плода и обратно") является неполным ответом. Неясно, знает ли учащийся, как можно рассчитать расстояние от датчика до поверхности плода, если известны скорость волны v и промежуток времени t.
Согласно пизовцам, российским школьникам достаточно угадывать "правильный": если известны расстояние и скорость, то что можно вычислить? Но как вычислить — это уже не нужно знать!
Пизовцы: "Правильный" ответ: Расстояние = скорость/время, хотя формула неверная, учащийся правильно указал, что нужно измерить «время».
Программа ПИЗА, в том числе такие задания и такие ответы (или подобными им) послужили обоснованием для модернизации российского образования!
ПРИЛОЖЕНИЕ № 1
ФИЗИЧЕСКИЕ ПРИНЦИПЫ УЛЬТРАЗВУКОВОГО МЕТОДА ИССЛЕДОВАНИЯ
Источник информации — http://www.ngmu.ru/cozo/images/demo/uzi/info/t1/1.htm
История открытия ультразвука
Ультразвуковой метод — способ дистантного определения положения, формы, величины, структуры и движения органов и тканей, а также выявления патологических изменений с помощью ультразвукового излучения.
Ультразвук в природе в 1794 г. открыл Спалланцани. Он заметил, что если летучей мыши заткнуть уши, она теряет ориентировку. Ученый предположил, что ориентация в пространстве осуществляется посредством излучаемых и воспринимаемых невидимых лучей.
В лабораторных условиях ультразвук впервые был получен в 1830 г. братьями Кюрие. После Второй мировой войны Холмес на основании принципа сонара — прибора, применявшегося в подводном флоте, сконструировал диагностические установки, получившие распространение в акушерстве, неврологии и офтальмологии.
В последующем совершенствование ультразвуковых аппаратов привело к тому, что данный метод в настоящее время стал самым распространенным при визуализации паренхиматозных органов.
Природа ультразвуковых колебаний
Ультразвуковые волны — это акустические волны, частота которых превышает частоту звука, слышимого человеческим ухом (свыше 20 кГц).
Ультразвук представляет собой механические колебания среды, поэтому для распространения ультразвуковой волны необходима упругая среда: жидкость, тканевая структура. Если среда не обладает упругими свойствами (вакуум) или упругие ее свойства незначительны (воздух), то ультразвук в ней не распространяется или распространение его затруднено. Поэтому при обследовании пациента на рабочую поверхность датчика наносится акустический гель, исключающий воздушную прослойку.
Частицы среды не перемещаются в направлении распространения волны, а колеблются около своих положений равновесия. В направлении распространения волны передается только энергия колебаний.
В зависимости от направления колебаний частиц относительно распространения волны различают несколько типов ультразвуковых волн: продольные, поперечные, изгибные, поверхностные и волны растяжения. В диагностической аппаратуре используют только продольные ультразвуковые колебания, так как только они распространяются в биологических средах. Остальные типы волн не распространяются в газах и большинстве жидкостей, ввиду того, что последние не обладают сдвиговой упругостью.
В продольных ультразвуковых волнах направление колебания частиц совпадает с направлением распространения волны. Структура продольной волны представляет собой чередование зон сжатия и разряжения. Продольные УЗ волны обладают высокой проникающей способностью и проходят через ткани организма.
Характеристика ультразвуковой волны
Для характеристики упругих волн, к которым относятся ультразвуковые колебания, применяют следующие основные параметры.
Частота колебаний (f) — это число колебаний или число чередований сжатий и разряжений в секунду. Она является одной из основных характеристик упругой волны. За единицу частоты колебаний принят герц (Гц), соответствующий одному колебанию в секунду, один килогерц (кГц) — 1000 колебаний в секунду, один мегагерц (МГц) — 1 000 000 колебаний в секунду. Колебания с частотой до 16 Гц называются инфразвуковыми ; от 16 Гц до 20 кГц — звуковыми ; больше 20 кГц — ультразвуковыми ; выше 109 Гц — гиперзвуковыми . Диапазон частот ультразвука, используемых в медицинской диагностике, лежит в пределах от 1 до 30 МГц.
Период колебаний (Т) — это время, необходимое для завершения полного цикла колебания. Эта величина обратно пропорциональна частоте колебаний.
Длина волны (λ)— это расстояние между двумя ближайшими точками среды, находящимися в одинаковой фазе колебания.
Скорость распространения волны (С) — это расстояние, на которое распространяется волна в единицу времени. Она тесно связана с частотой и периодом колебаний, а также с длиной волны.
Амплитуда колебаний — это высота ультразвуковой волны, которая характеризует максимальное смещение колеблющихся частиц среды от их положения покоя. Она определяет энергетическое состояние ультразуковых колебаний.
Частота, период и амплитуда ультразвукового излучения определяется источником ультразвука — ультразвуковым сканером. Врач ультразвуковой диагностики в зависимости от цели исследования, глубины расположения визуализируемого органа подбирает необходимые параметры ультразвукового излучения.
Скорость распространения ультразвука зависит от плотности среды. Скорости распространения ультразвуковой волны в некоторых средах:
- в воздухе — 343 м/с;
- в легких — 400 м/с;
- в воде — 1480 м/с;
- в мягких тканях и паренхиматозных органах от 1540 до 1620 м/с;
- в костной ткани — более 2500 м/с.
Усредненная скорость распространения ультразвука в тканях человека составляет 1540 м/с — на эту скорость запрограммировано большинство ультразвуковых диагностических приборов.
Свойства ультразвука
1. Отражение ультразвука. В ультразвуковых диагностических системах используется эхолокационный принцип получения информации об органах и структурах. Принцип работы диагностических приборов заключается в следующем: объект подвергают воздействию направленного УЗ луча и регистрируют эхосигналы, отраженные от границы двух сред с различной плотностью. На основе полученных данных строится акустическое изображение.
Эхосигналы — это отраженные сигналы, которые принимаются датчиком и используются для диагностики. При этом используются те отраженные волны, которые могут быть приняты датчиком, т. е. распространяющиеся только в сторону датчика.
Таким образом, отражение — основное физическое явление, на базе которого получается информация о тканях (рис. 1).

Рис. 1. Отражение и преломление ультразвука на границе сред
Если пучок ультразвуковых волн, распространяясь со скоростью С1 в однородной среде с плотностью р1, доходит до границы с другой средой, плотность которой р2, а скорость распространения в ней ультразвука С2, то часть энергии пройдет во вторую среду, а часть отразится от границы раздела. Количество отраженной энергии в этом случае определяется так называемым коэффициентом отражения (R), который рассчитывается по формуле:
R (%) = (р2С2— р1С1)(р2С2 + р1С1) × 100.
Скорость распространения ультразвуковых колебаний в различных органах и тканях практически одинакова (за исключением костей), близка к скорости распространения ультразвука в воде и в среднем составляет 1540 м/с. Таким образом, если С1 = С2 = 1540 м/с, то коэффициент отражения зависит только от плотности граничащих сред. Поэтому принято считать, что ультразвуковые волны отражаются от границы двух сред с различной акустической плотностью.
В табл. 1 представлены коэффициенты отражения на границе различных биологических сред.
Таблица 1
Коэффициент отражения ультразвука на границе биологических сред
Граница сред | Коэффициент отражения, % |
Кровь — мышца | 1,5 |
Кровь — почка | 2,1 |
Мышца — жир | 10,0 |
Печень — камни печени | 0-17,0 |
Мышца — кость | 64,0 |
Мягкие ткани — воздух | 99,95 |
Уровень отражения ультразвуковых волн на границе мягкая ткань — кость высокий и составляет 64 %, поэтому наблюдение структур, находящихся за костными тканями, затруднено. Отражение от границы мягкая ткань — камень также значительно и может меняться в широких пределах в зависимости от вида камня и его акустического сопротивления. Чем плотнее камень, тем больше уровень отражения на его границе и тем легче его обнаружить. При большой акустической плотности камня отражение от него может быть очень высокого уровня, так что в результате за ним образуется область акустической тени («ультразвуковая дорожка») — эхогенная зона, в которую ультразвуковые колебания не распространяются. Как известно, наличие акустической тени является одним из диагностических признаков наличия камня в органах.
Для мягких тканей коэффициент отражения не превышает 10 %, снижаясь иногда до нуля, если соседствующие ткани не отличаются по акустическому сопротивлению. Это означает, что только малая часть энергии падающей ультразвуковой волны вернется в виде отраженной ультразвуковой волны, а существенно большая часть будет распространяться вглубь тканей. В данном случае граница этих тканей не может быть обнаружена.
На границе мягкая ткань — воздух ультразвуковая волна отражается почти полностью (99,95 %), и дальше этой границы получить информацию невозможно. Вследствие этого газосодержащие структуры (легкие, желудок, кишечник), а также ткани, находящиеся за этими структурами, с помощью ультразвука исследовать невозможно, что является серьезным ограничением для ультразвуковой диагностики.
Таким образом, уровень отражения ультразвука зависит от степени акустической неоднородности граничащих тканей: чем выше различие в акустической плотности двух сред, тем больше волн отражается.
Кроме того, степень отражения зависит от угла падения ультразвукового луча на плоскость раздела сред — прямой угол дает наибольшее отражение. Если луч падает на границу двух сред под углом, отличным от прямого, то наряду с отражением наблюдается и преломление УЗ луча.
Преломление — изменение направления распространения волн при переходе из одной среды в другую, возникающее из-за разности скорости ультразвуковых волн в данных средах (рис. 1). При некоторой величине угла падения преломленный луч начинает скользить вдоль поверхности раздела, не проникая во вторую среду.
2. Поглощение ультразвука. По мере проникновения ультразвуковых волн в среду происходит снижение мощности ультразвукового излучения и затухание ультразвуковой волны. Это определяется расходом энергии волны на преодоление внутреннего трения, происходит поглощение ультразвука тканями.
Поглощение — переход энергии ультразвуковых волн в другие виды энергии, в частности, в тепло. Затухание ультразвуковой волны существенным образом влияет на качество акустического изображения.
Важнейшей характеристикой биологической среды является импеданс (Z). Он демонстрирует, какое сопротивление оказывает среда прохождению ультразвуковых волн. Акустический импеданс определяет собой отношение ультразвукового давления к колебательной скорости. В ограниченной среде импеданс представляет собой комплексную величину, в которой необходимо учитывать силы инерции, вязкости и упругости.
Получение ультразвука. Пьезоэлектрический эффект
Появление электрических импульсов на поверхности пьезокристалла при воздействии механических колебаний — называют прямым пьезоэлектрическим эффектом (дословно с греческого «давлю и получаю электричество»). Достоинство пьезоэлектрических преобразователей в том, что они являются и источником, и приемником ультразвуковых волн.
Таким образом, при воздействии на пьезокристалл переменным электрическим полем в нем возникают механические колебания (обратный пьезоэлектрический эффект), которые при соприкосновении со средой передаются в нее в виде упругих волн, частота которых зависит от частоты приложенного к пьезокристаллу переменного электрического поля. Эхосигналы, отраженные от неоднородностей биологической среды, воздействуя на пьезоэлемент, вызывают появление электрического разряда, который можно зарегистрировать.
Биологическое действие ультразвука
Биологическое действие излучения — это изменения в живых организмах, которые являются результатом воздействия излучения на ткани. В зависимости от частоты, интенсивности и времени экспозиции ультразвуковой волны могут быть безвредными (диагностический ультразвук), оказывать лечебное действие (ультразвуковое излучение, применяемое при физиотерапевтическом лечении) и вызывать патологические изменения в тканях. В основе вредного влияния ультразвука лежат термические, физико-химические и механические воздействия.
При прохождении ультразвуковых волн через биологические среды происходит их поглощение тканями организма. Часть энергии ультразвука переходит в тепловую энергию, что приводит к разогреву тканей. В начальной стадии гипертермического эффекта наблюдается расширение сосудов, ускорение кровотока и появление эритемы. Если температура повышается на 10° С, происходит возрастание активности большинства ферментов более чем в 2 раза. При повышении температуры до 50° С происходит инактивация ферментов, прекращение химических реакций и денатурация белков. Терапевтические и, тем более, диагностические дозы ультразвукового излучения не влияют на температуру тканей.
Физико-химическое действие ультразвука разнообразно. Под влиянием ультразвукового излучения происходит усиленное поглощение кислорода клетками крови, однако это не приводит к накоплению углекислоты, наоборот, ее концентрация снижается, чем, вероятно, и объясняется сдвиг рН крови в щелочную сторону. Ультразвук интенсивностью более 1 Вт/см2 приводит к накоплению в тканях ионов азотистой и азотной кислоты, которые способствуют диазотированию и нитрированию ароматических кислот, входящих в состав белковых молекул. Ультразвуковое излучение мощностью 0,6 Вт/см2вызывает конформационную перестройку клеточных мембран и нарушение их проницаемости. Это приводит к накоплению в клетках ионов натрия и кальция и к потере ионов калия, что, в свою очередь, вызывает нарушение процессов поляризации и деполяризации.
При мощности ультразвуковых колебаний 1,5-3,5 Вт/см2возникают некрозы тканей. Наибольшее повреждающее действие ультразвука обусловлено кавитацией. Сущность этого явления состоит в том, что под влиянием ультразвуковых колебаний большой мощности и частоты происходит значительное увеличение амплитуды и скорости колебания частиц среды. Это приводит к тому, что в фазе разряжения в жидких и коллоидных биологических средах возникают мелкие полости (разрывы) в виде пузырьков, содержащих пары жидкости и газа. Затем в фазе сжатия происходит исчезновение этих полостей, сопровождающиеся гидравлическими ударами большой разрушительной силы. Кавитация в биологических средах возникает при интенсивности ультразвукового излучения более 3-5 Вт/см2 .
Большим количеством исследований установлено, что ультразвук интенсивностью 0,1 Вт/см2не оказывает отрицательного влияния на ткани организма. В клинической практике преимущественно используются терапевтические мощности ультразвука 0,05-0,5 Вт/см2. Средняя интенсивность энергии ультразвуковых волн, используемых в диагностике, не превышает 0,01 Вт/см2, что значительно ниже энергии, которая сопровождается механической и химической реакцией тканей. Ультразвуковые волны в диапазоне, применяемом в диагностике, не вызывают выраженных биологических эффектов.
В специальных многолетних клинических наблюдениях существенных вредных последствий от ультразвуковых исследований не зарегистрировано, безопасность этого метода подтверждена также экспериментальными данными. Исследования, связанные с воздействием ультразвука на клетки, экспериментальные работы на растениях и животных, а также эпидемиологические исследования позволили сделать Американскому институту ультразвука следующее заявление: «Никогда не сообщалось о подтвержденных биологических эффектах у пациентов или лиц, работающих на приборе, вызванных облучением ультразвуком, интенсивность которого типична для современных ультразвуковых диагностических установок. Хотя существует возможность, что такие биологические эффекты могут быть в будущем, современные данные указывают, что польза для больного при благоразумном использовании диагностического звука перевешивает потенциальный риск, если таковой вообще существует».
Однако специалист ультразвуковой диагностики должен помнить о биологических эффектах взаимодействия ультразвука с тканями и соблюдать рекомендации, направленные на максимальное снижение возможного отрицательного воздействия:
- разумное уменьшение уровня выходной мощности;
- фиксация изображения сразу после получения требуемой диагностической информации;
- проведение всего исследования в кратчайшие сроки, достаточные для постановки диагноза.
ПРИЛОЖЕНИЕ № 2
Равномерное и равноускоренное прямолинейное движение
Источник информации — http://www.edu.yar.ru/russian/projects/socnav/prep/phis001/kin/kin2.html (Социальный навигатор — «Здесь вам помогут»)
Кинематика — http://www.edu.yar.ru/russian/projects/socnav/prep/phis001/kinematics.html
Равномерное прямолинейное движение. Скорость
Равномерным прямолинейным движением называют такое происходящее по прямолинейной траектории движение, при котором тело (материальная точка) за любые равные промежутки времени совершает одинаковые перемещения.
Перемещение тела в прямолинейном движении обычно обозначают s. Если тело движется по прямой только в одном направлении, модуль его перемещения равен пройденному пути, т.е. |s| = s. Для того, чтобы найти перемещение тела s за промежуток времени t, необходимо знать его перемещение за единичное время. С этой целью вводят понятие скорости v данного движения.
Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение:
Направление скорости в прямолинейном движении совпадает с направлением перемещения.
Поскольку в равномерном прямолинейном движении за любые равные промежутки времени тело совершает равные перемещения, скорость такого движения является величиной постоянной (v=const). По модулю
Из формулы (1.2) устанавливают единицу скорости.
В настоящее время в качестве основной системы единиц используют Международную систему единиц (сокращенно СИ — система интернациональная). Об этой системе рассказано далее. Единицей скорости в СИ является 1 м/с (метр в секунду); 1 м/с есть скорость такого равномерного прямолинейного движения, при котором материальная точка за 1 с совершает перемещение 1 м.
Пусть ось Ох системы координат, связанной с телом отсчета, совпадает с прямой, вдоль которой движется тело, а x0 является координатой начальной точки движения тела. Вдоль оси Ох направлены и перемещение s, и скорость v движущегося тела. Из формулы (1.1) следует, что s = vt. Согласно этой формуле, векторы s и vt равны, поэтому равны и их проекции на ось Ох:
Теперь можно установить кинематический закон равномерного прямолинейного движения, т. е. найти выражение для координаты движущегося тела в любой момент времени. Поскольку х = x0+sx, с учетом (1.3) имеем
По формуле (1.4), зная координату x0 начальной точки движения тела и скорость тела v (ее проекцию vx на ось Ох), в любой момент времени можно определить положение движущегося тела. Правая часть формулы (1.4) является алгебраической суммой, так как и х0, и vx могут быть и положительными, и отрицательными (графическое представление равномерного прямолинейного движения дано далее).
Средняя и мгновенная скорости
прямолинейного неравномерного движения
Движение, при котором за равные промежутки времени тело совершает неравные перемещения, называют неравномерным (или переменным). При переменном движении скорость тела с течением времени изменяется, поэтому для характеристики такого движения введены понятия средней и мгновенной скоростей.
Средней скоростью переменного движения vcp называют векторную величину, равную отношению перемещения тела s к промежутку времени t, за который было совершено это перемещение:
Средняя скорость характеризует переменное движение в течение только того промежутка времени, для которого эта скорость определена. Зная среднюю скорость за данный промежуток времени, можно определить перемещение тела по формуле s = vср·t лишь за указанный промежуток времени. Найти положение движущегося тела в любой момент времени с помощью средней скорости, определяемой по формуле (1.5), нельзя.
Как указывалось выше, когда тело движется по прямолинейной траектории в одну сторону, модуль его перемещения равен пройденному телом пути, т.е. |s| = s. В таком случае среднюю скорость определяют по формуле v = s/t, откуда имеем
Мгновенной скоростью переменного движения называют скорость, которую тело имеет в данный момент времени (и следовательно, в данной точке траектории).
Выясним, каким способом можно определить мгновенную скорость тела. Пусть тело (материальная точка) совершает прямолинейное неравномерное движение. Определим мгновенную скорость v этого тела в произвольной точке С ее траектории (рис. 2).

Выделим маленький участок Ds1 этой траектории, включающий в себя точку С. Этот участок тело проходит за промежуток времени Dt1. Разделив Ds1 на Dt1, найдем значение средней скорости vcp1 =Ds1/Dt1 на участке Ds1. Затем для промежутка времени Dt2<Dt1 определим среднюю скорость vcp2 =Ds2/Dt2 на участке Ds2<Ds1. Затем для промежутка времени Dt3<Dt2 определим среднюю скорость vcp3 =Ds3/Dt3 на участке Ds3 и т.д. (участки траектории мы выбираем так, что точка С всегда находится внутри рассматриваемого участка).
Очевидно, что чем меньше промежуток времени Dt, тем меньше длина участка Ds, проходимого телом, и тем меньше значение средней скорости vcp=Ds/Dt отличается от значения мгновенной скорости в точке С. Если промежуток времени Dt стремится к нулю, длина участка пути Ds бесконечно уменьшается, а значение средней скорости vcp на этом участке стремится к значению мгновенной скорости в точке С. Следовательно, мгновенная скорость v есть предел, к которому стремится средняя скорость тела vcp, когда промежуток времени движения тела стремится к нулю:
Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю (если этот предел существует), представляет собой первую производную этой функции по данному аргументу. Поэтому формулу (1.7) запишем в виде
где символы d/dt или штрих справа вверху у функции обозначают производную этой функции. Следовательно, мгновенная скорость есть первая производная пути по времени.
Если аналитический вид зависимости пути от времени известен, с помощью правил дифференцирования можно определить мгновенную скорость в любой момент времени. В векторной форме
Равноускоренное прямолинейное движение. Ускорение
Такое прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, называют равноускоренным прямолинейным движением.
Быстроту изменения скорости характеризуют величиной, обозначаемой а и называемой ускорением. Ускорением называют векторную величину, равную отношению изменения скорости тела v-v0 к промежутку времени t, в течение которого это изменение произошло:
Здесь V0 — начальная скорость тела, т. е. его мгновенная скорость в момент начала отсчета времени; v — мгновенная скорость тела в рассматриваемый момент времени.
Из формулы (1.9) и определения равноускоренного движения следует, что в таком движении ускорение не изменяется. Следовательно, прямолинейное равноускоренное движение есть движение с постоянным ускорением (a=const). В прямолинейном равноускоренном движении векторы v0, v и а направлены по одной прямой. Поэтому модули их проекций на эту прямую равны модулям самих этих векторов, и формулу (1.9) можно записать в виде
Из формулы (1.10) устанавливается единица ускорения.
В СИ единицей ускорения является 1 м/с2 (метр на секунду в квадрате); 1 м/с2 — это ускорение такого равноускоренного движения, при котором за каждую секунду скорость тела увеличивается на 1 м/с.
Формулы мгновенной и средней скоростей
равноускоренного движения
Из (1.9) следует, что v = v0 + at.
По этой формуле определяют мгновенную скорость v тела в равноускоренном движении, если его начальная скорость v0 и ускорение а известны. Для прямолинейного равноускоренного движения эту формулу можно записать в виде
Если v0 = 0, то
Получим выражение для средней скорости прямолинейного равноускоренного движения. Из формулы (1.11) видно, что v=v0 при t = 0, v1 = v0 + a при t = 1, v2 = v0 + 2a = v1 + a при t = 2 и т. д. Следовательно, в равноускоренном движении значения мгновенной скорости, которые тело имеет через равные промежутки времени, образуют такой ряд чисел, в котором каждое из них (начиная со второго) получается путем прибавления к предшествующему постоянного числа а. Это значит, что рассматриваемые значения мгновенной скорости образуют арифметическую прогрессию. Следовательно, средняя скорость прямолинейного равноускоренного движения может быть определена по формуле
где v0 — начальная скорость тела; v — скорость тела в данный момент времени.
Уравнение равноускоренного прямолинейного движения
Найдем кинематический закон прямолинейного равноускоренного движения. Для этого используем формулы (1.6), (1.11) и (1.13). Из них следует, что s = vср·t = (v0 + v)·t/2 = (2v0 + at)·t/2,
следовательно,
Если начальная скорость тела равна нулю (v0 = 0), то
По формулам (1.14) и (1.15) определяют путь, пройденный телом в равноускоренном прямолинейном движении (модуль перемещения тела, не изменяющего направления своего движения). Для случая, когда тело движется по оси Ох. из точки с координатой х0, из формулы (1.14) получаем уравнение, выражающее зависимость координаты этого тела от времени. Поскольку
имеем
Формула (1.16) есть уравнение прямолинейного равноуско-ренного движения (кинематический закон этого движения). Следует помнить, что в формуле (1.16) v0x и аx могут быть как положительными, так и отрицательными, так как это проекции векторов v0 и а на ось Ох.
Связь перемещения тела с его скоростью
Установим связь модуля перемещения s тела, совершающего равноускоренное прямолинейное движение, с его скоростью. Из формулы (1.10) находим, что t=(v-v0)/a. Подставив это выражение и формулу (1.13) в формулу (1.7), получим
следовательно,
Если начальная скорость тела равна нулю (v0 = 0), то v2 = 2as.
ПРИЛОЖЕНИЕ № 3
Задачи
Источник информации — http://www.physbook.ru/index.php/Задачи._Равноускоренное_движение
Уровень А
Задача № 1. Куда направлены ускорения следующих тел:
а) у поезда, который начинает тормозить;
б) у поезда, который отходит от станции?
Решение задачи № 1.
а) У поезда, который начинает тормозить, скорость уменьшается, поэтому ускорение направлено против движения;
б) у поезда, который отходит от станции, скорость увеличивается, поэтому ускорение направлено вдоль движения.
Задача № 2. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?
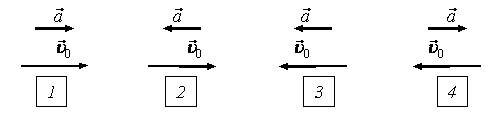
Решение задачи № 2
Направление движения определяем по направлению скорости, изменение скорости – по направлению ускорения и скорости.
Тело 1 движется вправо; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.
Тело 2 движется вправо; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.
Тело 3 движется влево; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.
Тело 4 движется влево; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.
Задача № 3. Скорость движения автомобиля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение автомобиля.
Решение задачи № 3
| t = 40 c; |
| υ0 = 5 м/с; |
| υ = 15 м/с; |
| a – ? |
Скорость автомобиля увеличивается, поэтому ускорение направлено в сторону движения. Ускорение автомобиля , где υx = υ ; υ0x = υ0 , т.к. скорости направлены вдоль оси 0Х (рис. 1). Тогда
; ax = (15 м/с — 5 м/с)/40 с = 0,25 м/с2.
Ответ. Ускорение равно 0,25 м/с2, направлено в сторону движения.
Проверка ответа: скорость тела увеличивается, поэтому проекция ускорения на данную ось должна быть положительная, что соответствует ответу.
Задача № 4. С каким ускорением двигался автобус, если, трогаясь с места стоянки, он развил скорость 15 м/с за 50 с?
Решение задачи № 4
| t = 50 c; |
| υ = 15 м/с; |
| a – ? |
Скорость автобуса увеличивается, поэтому ускорение направлено в сторону движения. Ускорение автобуса , где υx = υ , т.к. скорость направлена вдоль оси 0Х (рис. 1); υ0x = υ0 = 0 («скрытые данные»), т.к. автобус «трогается с места». Тогда
; ax = 15 (м/с)/50 с = 0,3 м/с2.
Ответ. Ускорение равно 0,3 м/с2, направлено в сторону движения.
Проверка ответа: скорость тела увеличивается, поэтому проекция ускорения на данную ось должна быть положительная, что соответствует ответу.
ВНИМАНИЕ!
РЕШЕНИЕ СЛЕДУЮЩИХ ЗАДАЧ СМОТРИТЕ
на сайте: http://www.physbook.ru/index.php/Задачи._Равноускоренное_движение
5. Двигаясь со скоростью 72 км/ч, мотоциклист притормозил и через 20 с достиг скорости 36 км/ч. С каким ускорением он тормозил?
6. Поезд подходит к станции со скоростью 21,6 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?
7. В начале измерения скорость тела равнялась 5 м/с и направлена была на север. Через 50 с измерения показали, что тело двигается со скоростью 15 м/с на юг. Считая движения тела равноускоренным прямолинейным, определите его ускорение.
8. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с2. Через сколько времени он приобретет скорость 54 км/ч?
9. Через сколько времени останавливается автобус, если его начальная скорость 20 м/с, а ускорение 1,25 м/с2?
10. Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
11. Какую скорость приобретает отходящий от станции поезд через 7 с от начала движения, если его ускорение равно 0,9 м/с2?
12. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с2 через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?
13. Определите скорость тела при торможении с ускорением 0,2 м/с2 через 30 с от начала торможения, если начальная скорость его была равна 2 м/с.
14. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался с ускорением 9,8 м/с2?
15. Тело движется прямолинейно равнозамедленно с начальной скоростью 10 м/с и ускорением 2 м/с2. Определите перемещение тела через 5 с после начала движения.
16. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с2?
17. Пассажирский поезд тормозит с ускорением 0,2 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 54 км/ч?
18. Автобус движется со скоростью 36 км/ч. На каком расстоянии от остановки водитель должен начать тормозить, сообщая автобусу ускорение,
не превышающее 1,2 м/с2?
19. Автомобиль движется прямолинейно с постоянным ускорением 2,0 м/с2, имея в данный момент скорость 10 м/с. Где он был 4,0 с назад?
20. Поезд, движущийся после начала торможения с ускорением 0,40 м/с2, через 15 с имел скорость 10 м/с. Найдите пройденный путь за это время.
21. Снаряд, летящий со скоростью 1000 м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200 м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.
22. После старта гоночный автомобиль достиг скорости 360 км/ч за 25 с. Какое расстояние он прошел за это время?
23. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь.
Уровень B
1. Шарик скатывается по желобу длиной 1,25 м с ускорением 1,6 м/с2. Какова скорость шарика в конце жалоба?
2. Хоккейная шайба пересекла ледяное поле длиной 60 м за 3,0 с и остановилась. Какая скорость была сообщена шайбе клюшкой хоккеиста?
3. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с2, пройдет 30 м?
4. Самолет при отрыве от земли имеет скорость 252 км/ч и пробегает по бетонированной дорожке расстояние 700 м. Сколько времени продолжает разбег самолет? Движение считайте равноускоренным.
5. Ножной тормоз грузового автомобиля считается исправным если при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее этой норме тормозное ускорение.
6. При какой начальной скорости поезд пройдет путь 1260 м в течении 60 с, замедляя ход с ускорением 1,5 м/с2?
7. Электропоезд тормозит с ускорением 0,40 м/с2. Определите, за какое время он остановится, если тормозной путь равен 50 м.
8. Лифт Останкинской телевизионной башни заканчивает свое движение после прохождения 49 м за 14 с. Найдите ускорение и начальную скорость лифта.
9. Поезд, двигаясь с горы с ускорением 0,2 м/с2, прошел путь 340 м и развил скорость 19 м/с. Сколько времени двигался поезд и какой была его скорость в начале отсчета?
10. Поезд, движущийся после начала торможения с ускорением 0,40 м/с2, через 25 с остановился. Найдите скорость в момент начала торможения и тормозной путь.
ПРИЛОЖЕНИЕ № 4
Задачи по применению математических знаний в различных сферах деятельности
(Задачи на определение математической грамотности)
Предисловие А.В. Краснянского
Деятели программы PISA используют новые термины "математическая грамотность", "естественнонаучная грамотность", "грамотность чтения", но возникновение этих терминов не связано с открытием нового знания в педагогике. В советских и российских учебниках были и есть толковые задачи на применение математических знаний в быту и в профессиональной деятельности. Здесь представлены задачи для 2, 3 и 5 классов, часть которых решаются в два-три действия. Показательно, что некоторые задания (для пятнадцатилетних учащихся — 9 и 10 класс!) международной программы PISA решаются в одно (!) действие.
Задачи для 2 класса
Источник информации: Б.П. Гейдман, Т.В. Ивакина, И.Э. Мишарина. Математика. Учебник для второго класса начальной школы. Первое полугодие. Допущено Министерством образования и науки Российской Федерации. Москва. Издательство МЦНМО. Издательство «Русское слово». 2007.
№ 10 (стр. 76.) Капроновый шнур длиной 30 м разрезали на 3 части, причем одна из них на 1 м больше другой и на 1 м меньше третьей. Найди длину каждой части шнура.
№ 6 (стр. 82.) На строительстве одного дома работали 28 рабочих, это на 15 человек меньше, чем на строительстве другого дома. Сколько всего рабочих строило эти два дома?
№ 8 (стр. 84.) Для окраски стен детского сада потребовалось 15 кг желтой краски, что на 17 кг меньше, чем светло-голубой, а бледно-зеленой на 9 кг меньше, чем светло-голубой. Сколько потребовалось бледно-зеленой краски для окраски стен детского сада?
№ 7 (стр. 96.) Если расходовать одно и то же количество воды каждый день, то 16 л хватит на 2 дня. На сколько дней хватит 24 л ключевой воды при таком же ежедневном расходе?
№ 7 (стр. 108.) Перед поездкой на дачу в баке машины было 10 л бензина. На автозаправке папа залил в бак еще 30 л. Когда же он приехал на дачу, в баке осталось 27 л. Сколько литров бензина было израсходовано?
№ 8 (стр. 108.) В бочке 50 л бензина. Когда из бочки перелили какое-то количество бензина в бак, то в баке и бочке стало по 35 л бензина. Сколько литров бензина было в баке первоначально?
Задачи для 3 класса
Источник информации: М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, Н.Ф. Вапняр, С.В. Степанова. Математика. 3 класс. Учебник для четырехлетней начальной школы. Под редакцией Ю.М. Колягина. Утверждено Министерством образования РСФСР. 5-е издание, переработанное. Москва. «Просвещение». 1992.
№ 4 (стр. 108.) Сколько масла получится из 75 л молока, если из 50 л молока получается 2 кг масла?
№ 5 (стр. 108.) Для ремонта дороги участок, имеющий форму прямоугольника, обнесли забором из деревянных щитов. Сколько таких щитов потребовалось, если длина участка 6 м, ширина 4 м, а длина одного щита равна 2 ?
№ 6 (стр. 109.) Мастер обрабатывал деталь на старом станке за 12 минут, а на новом станке – за 8 минут. Сколько времени экономит мастер при обработке 1 такой детали? 4 деталей? 8 деталей?
№ 4 (стр. 111.) Дневная норма выработки у рабочего была 20 деталей. На новом станке он за 2 дня изготовил 80 деталей. Во сколько раз больше деталей изготовил рабочий за день на новом станке?
№ 8 (стр. 113.) 16 кг муки расфасовали поровну в 8 пакетов. Сколько таких пакетов потребуется для расфасовки 80 кг муки?
№ 3 (стр. 119.) В пекарне за 3 дня израсходовали 48 мешков муки. На сколько дней хватит 80 мешков муки, если каждый день будет расходоваться одинаковое количество муки?
№ 5 (стр. 121.) В ящик уложили помидоры. Масса помидоров 18 кг, а масса ящика в 9 раз меньше. Чему равна масса ящика, наполненного помидорами?
№ 6 (стр. 121.) В мягком вагоне поезда 36 спальных мест. Продано 60 билетов для проезда в 2 мягких вагонах. Сколько еще билетов можно продать в эти вагоны?
№ 7 (стр. 123.) С трех овец настригли в год 18 кг шерсти (с каждой поровну). Сколько шерсти можно настричь с 10 таких овец? с 12 овец?
№ 8 (стр. 125.) (Устно.) Нужно вывезти из леса 35 больших бревен. Трактор за 1 раз вывозит по 9 бревен. Сколько раз трактору нужно съездить в лес? Сколько бревен он привезет в последний раз?
№ 4 (стр. 126.) Грузовая машина израсходовала до остановки 48 л горючего, а после остановки 32 л. Сколько всего часов была машина в пути, если за 1 час расходовалось 16 л горючего?
№ 4 (стр. 130.) Отец и сын окапывали кусты смородины. Отец в час окапывал 5 кустов, а сын 3. Сколько времени они должны работать вместе, чтобы окопать 24 куста?
№ 6 (стр. 139.) За 7 часов токарь изготовил 84 одинаковые детали. Сколько часов ему потребуется для изготовления 72 таких деталей при той же норме выработки?
№ 3 (стр. 142.) За 7 дней хозяйка израсходовала 14 кг картофеля. Сколько килограммов картофеля надо на 28 дней, если каждый день расходовать столько же, сколько раньше?
№ 3 (стр. 143.) В теплице собрали 96 кг помидоров и разложили в ящики, по 6 кг в каждый. Все помидоры отправили для продажи в два ларька. Сколько ящиков получил первый ларек, если второй получил 10 ящиков?
№ 11 (стр. 146.) Из 1 кг помидоров получили 4 г семян. Сколько штук семян получили, если в одном грамме их насчитывается 250 штук?
№ 2 (стр. 161.) В мебельном магазине 30 покупателей купили по 4 книжные полки и 20 покупателей по 8 полок. Сколько всего полок купили эти покупатели?
№ 2 (стр. 169.) На старом станке токарь изготовил за 6 часов 96 деталей, а на новом станке ту же норму сделал за 4 часа. На сколько деталей больше стал изготавливать токарь за 1 час?
№ 4 (стр. 173.) В одну столовую привезли 40 банок огурцов, по 5 кг в каждой, а в другую 50 банок по 3 кг в каждой. Сколько всего огурцов привезли в обе столовые?
№ 3 (стр. 174.) Из совхоза в город отправили молоко: машину-цистерну емкостью 500 л и еще 9 бидонов молока, по 40 л в каждом. Сколько всего литров молока отправили в город?
№ 4 (стр. 178.) По заданию заводы школьникираскладывали детали в коробки, по 6 деталей в каждую коробку. Они уже уложили 50 коробок. Сколько деталей им осталось разложить, если всего было 372 детали?
№ 32 (стр. 185.) В театральной кассе было 480 билетов. Кассир продал билеты на 5 спектаклей, по 16 билетов на каждый. Сколько билетов осталось в кассе?
№ 35 (стр. 185.) Маляр покрасил 24 парты за 2 дня, поровну каждый день. За сколько дней он покрасит 60 парт, работая так же?
Задачи для 5 класса
Источник информации: Э.Р. Нурк, А.Э. Тельгмаа. Математика. Учебник для 5 класса. Утверждено Государственным комитетом СССР по народному образованию. 2-е издание. Москва. «Просвещение». 1990
494. Длина одной стороны земельного участка прямоугольной формы 125 м и площадь его 105000 м2. Вычисли периметр этого участка.
668. Участок прямоугольной формы обнесен забором. Через каждые 2 м забора врыт столб. Сколько всего столбов в заборе, если длина одной стороны участка 80 м, а длина другой на 40 м больше.
683. В двухкомнатной квартире ширина каждой комнаты 4 м, а их длина 7 м и 5 м. Сколько квадратных метров коврового покрытия потребуется, чтобы полностью застлать полы в комнатах?
686. Прямоугольные плиты для застилки дорожки имеют размеры 180 см и 50 см. Сколько потребуется плит, чтобы застелить дорожку длиной 450 м и шириной 180 см?
687. Два земельных участка прямоугольной формы имеют площадь 1728 м2. Стороны одного участка 24 м и 16 м, длина второго участка 42 м. Вычисли ширину второго участка.
1059. Длина ячменного поля прямоугольной формы 625 м, а ширина на 177 м меньше. С этого поля собрали урожай 42,7 ц с каждого гектара. Сколько центнеров ячменя собрали со всего поля?
1211. Сколько кирпичей в штабеле?

1215. Посеяли ячмень на участке 6 га без удобрений и на участке 7,5 га на хорошо удобренной почве. С неудобренного участка получили 100,8 ц, а с удобренного 405 ц ячменя. Как сказалось наличие удобрений в почве на урожайности ячменя?
1218. Остров Комсомолец, площадь которого 9600 км2, и остров Пионер, площадь которого составляет примерно 17 % площади острова Комсомолец, принадлежит архипелагу Северная Земля. Вычисли площадь острова Пионер. Ответ округли до сотен.
1251. Длина деревянного бруса 4 м, ширина 2 дм и толщина 1 дм. Чему равна его масса, если масса 1 дм3 дерева равна 0,65 кг?
1252. Воздух объемом 1 м3 имеет массу 1,29 кг. Какова масса воздуха в классной комнате, если ее длина 8,2 м, ширина 5,5 м и высота 3 м? Ответ округли до единиц.
1254. На сельскохозяйственных работах использовали новый грузовой автомобиль. Длина его кузова 4,4 м, ширина 2,3 м и высота 0,68 м. После увеличения высоты бортов объем кузова стал в два раза больше. Вычисли объем кузова до и после надстройки. Ответ округли до единиц.
1260. Сенохранилище имеет форму прямоугольного параллелепипеда с измерениями 16,5 м, 5,2 м и 4 м. Сколько тонн сена может поместиться в хранилище, если 1 м3 сена имеет массу 54 кг?
1283. Экскаватор выкопал яму, имеющую форму куба. Ребро этого куба равно 4 м. Сколько автомашин потребуется, чтобы вывезти всю землю, если одна машина вмещает 2,5 м3 земли?
1284. Из алюминия изготовили деталь в форме прямоугольного параллелепипеда с измерениями 6 см, 8 см и 15 см, а из железа – куб с ребром 7 см. Масса 1 см3 алюминия 2,7 г, а 1 см3 железа 7,8 г. Сравни массы этих деталей.
1286. Товарный контейнер имеет форму куба, ребро которого 2 м. В этот контейнер нужно загрузить максимальное количество ящиков, имеющих форму прямоугольного параллелепипеда с измерениями 0,4 м, 0,5 м и 0,2 м. Сколько ящиков можно загрузить в контейнер? Объясни, как их разместить.
1306. Приготовили два ящика промышленных отходов. Один в форме прямоугольного параллелепипеда с измерениями 2,6 м, 1,4 м и 0,8 м, а другой в форме куба с ребром 13 дм. В какой из ящиков поместится больше отходов?
1338. Хранилище автомобильного масла имеет форму прямоугольного параллелепипеда, измерения которого 2,5 м, 1,6 м и 0,8 м. Сколько литров масла вмещает хранилище?
1339. 1 дм3 железа имеет массу 7,8 кг. Какова масса двухметрового железного бруса, если его сечение – квадрат со стороной 5 см.
1420. В грузовую машину можно уложить 35 ящиков с товаром, каждый вместимостью 48,2 кг, и 80 ящиков вместимостью 12,6 кг каждый. Вычисли массу товара, нагруженного в машину (в тоннах).
1437. Вычисли общий объем всех ящиков, имеющих форму куба (рис.6.6), если ребро каждого куба 0,5 м.

1451. С одного поля площадью 3 гектара собрали 9,6 т ячменя, а с другого поля площадью 9 гектар собрали 36,9 т. Вычисли средний урожай ячменя с одного гектара. Ответ округли до десятых тонны. (Редакция А.К.)
1453. Требуется обнести проволочной сеткой высотой 1,2 м сад четырехугольной формы, стороны которого 27 м, 33 м, 22 м и 19 м. Сколько потребуется квадратных метров сетки?
1457. Сторона квадратного жестяного листа равна 1,5 м. Лист нужно разрезать на куски прямоугольной формы с измерениями 1 м и 0,2 м. Выясни с помощью чертежа, как получить наибольшее количество прямоугольников.
1459. Измерения прямоугольного параллелепипеда, сделанного из ясеня, 8 см, 6 см и 4 см. Ребро куба, сделанного из бальзового дерева, 12 см. Масса 1 см3 ясеня 0,75 г, а 1 см3 бальзового дерева 0,25 г. Сравни объемы и массы прямоугольного параллелепипеда и куба.