Дмитрий Алексеевич Гусев. Удивительная логика.

Дмитрий Алексеевич Гусев

Удивительная логика

Источник информации — http://biologo.ru/Удивительная_логика/index6.html#pages      (Дата обращения 8 июня 2018 года).

Предисловие

Приходилось ли вам читать научно-популярную или учебную книгу с чувством, что вы не совсем понимаете, что в ней написано? Если да, то, скорее всего, исходя из «презумпции невиновности автора», вы вините в этом себя: за свой недостаточно высокий уровень образования, узость кругозора, отсутствие необходимых способностей. Однако правильнее было бы исходить из «презумпции собственной невиновности», так как если вы внимательно вчитываетесь, но не понимаете адресованный вам (согласно книжной аннотации) текст, то виноваты в этом не вы, а автор. Ведь он взялся написать книгу для вас, а не для самого себя или узкого круга своих коллег. Однако для доходчивого и внятного изложения материала ему не хватило логической культуры.

Что такое логическая культура? Это знание и соблюдение основных принципов и требований правильного построения и выражения мыслей как в устной, так и в письменной речи. Отсутствие такой культуры приводит к разнообразным логическим ошибкам, которые засоряют не только научное, но и повседневное мышление, мешают нам думать, общаться, понимать друг друга и самих себя. Неясность и неопределенность мышления, его непоследовательность и сумбурность, противоречивость и необоснованность является прямым результатом отсутствия должного уровня логической культуры.

Мышление, соответствующее требованиям логики, подобно прозрачному ручью: сквозь воды которого виден каждый камушек и песчинка на дне. Мышление, построенное на нарушениях логических законов, подобно мутному потоку: в нем ничего не видно. Правда, некоторые говорят, что в мутной воде удобнее «ловить рыбу», то есть строить такие высказывания и создавать такие тексты – сложные и малопонятные для адресата, – в которых внешняя глубокомысленность и наукообразность маскируют внутреннюю непоследовательность и порой – бессодержательность. Вряд ли добросовестный человек может быть сторонником такой «рыбалки».

Я взялся написать книгу не для себя, а для читателя, который начинает осваивать логику «с нуля». Насколько мне это удалось – судить читателю.

Книга состоит из пяти глав и ста занимательных задач. Первые три главы посвящены формам мышления, в которых выражается весь бесконечный по содержанию мир наших мыслей: понятию, суждению и умозаключению. В четвертой главе идет речь об основных законах логики и их распространенных нарушениях. Пятая глава посвящена условиям и приемам ведения дискуссии. Примеры, приводимые в книге, призваны показать, что логика – это не старая, сухая и безжизненная премудрость, а наука вечно молодая, полезная и даже интересная, которая вполне может помочь человеку в жизни.

Сто занимательных логических задач, завершающих книгу, различаются как по типу своего построения, так и по уровню сложности. Для их правильного решения требуется нестандартный подход и творческая работа мысли. Задачи направлены на развитие мышления, памяти, внимания и воображения; они помогут интересно и с пользой провести досуг. Для решения задач не обязательны теоретические знания по логике, достаточно жизненного опыта и смекалки, то есть интуитивной логики, которой в большей или меньшей степени обладают все люди, независимо от пола, возраста и уровня образования. Ко всем задачам приводятся ответы и комментарии. Однако не спешите в них заглядывать, попробуйте «поломать голову» и справиться с ними без всяких подсказок – чтобы испытать радость самостоятельного решения.

Введение

Логика – это наука о формах и законах правильного мышления. Она появилась приблизительно в IV веке до н. э. в Древней Греции. Ее создателем считается знаменитый древнегреческий философ и ученый Аристотель. Как видим, логике примерно 2,5 тысячи лет. Однако она до сих пор сохраняет свое практическое значение. Многие науки и искусства Древнего мира навсегда ушли в прошлое и представляют для нас только «музейное» значение, интересны исключительно как памятники старины, но некоторые из них пережили века, и в настоящее время мы продолжаем ими пользоваться. К их числу относятся геометрия Евклида (в школе мы изучаем именно ее) и логика Аристотеля, которая также называется традиционной логикой. В XIX веке появилась и стала быстро развиваться символическая (или математическая) логика. В традиционной логике для исследования правильного мышления используется естественный язык (тот, на котором мы говорим, пишем, читаем), а в символической логике – искусственный язык, или язык символов, подобный языку математики. Символическая логика – достаточно специфическая и непростая наука, ее можно рассматривать как раздел математики и информатики. Аристотелевская логика, напротив, будучи более широкой, представляет собой своего рода универсальную науку: ее освоение одинаково полезно и даже необходимо каждому человеку, независимо от того, какие области знания и предметы являются для него более близкими – социально-гуманитарные, естественно-математические или технические. Поэтому наша книга посвящена аристотелевской, или традиционной, логике.

Так зачем нам нужна логика, какую роль она играет в нашей жизни? Логика помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше понимать собеседника, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях.

Логическая культура – это знание и соблюдение основных принципов и требований правильного построения и выражения мыслей как в устной, так и в письменной речи. Отсутствие такой культуры приводит к многочисленным и разнообразным логическим ошибкам, которые засоряют не только научное, но и повседневное мышление, мешают нам думать, общаться, понимать друг друга и самих себя. Неясность и неопределенность мышления, его непоследовательность и сумбурность, противоречивость и необоснованность являются прямым результатом отсутствия должного уровня логической культуры.

Каждый из нас хорошо знает, что по содержанию человеческое мышление бесконечно многообразно, ведь мыслить (думать) можно о чем угодно, например, об устройстве мира и происхождении жизни на Земле, о прошлом человечества и его будущем, о прочитанных книгах и просмотренных фильмах, о сегодняшних занятиях и завтрашнем отдыхе… Но самое главное заключается в том, что наши мысли возникают и строятся по одним и тем же законам, подчиняются одним и тем же принципам, укладываются в одни и те же схемы или формы. Причем если содержание нашего мышления чрезвычайно разнообразно, то форм, в которых выражается это разнообразие, совсем немного.

Приведем простой пример. Рассмотрим три высказывания: Все караси – это рыбы; Все треугольники – это геометрические фигуры; Все стулья – это предметы мебели. Несмотря на различное содержание, у этих высказываний есть нечто общее, что-то их объединяющее. Что же это? Их объединяет форма. Отличаясь по содержанию, они сходны по форме, ведь каждое из трех высказываний строится по форме Все А – это В, где А и В – какие-либо объекты. Понятно, что само высказывание Все А – это В лишено всякого содержания. Это высказывание представляет собой чистую форму, которую можно наполнить любым содержанием, например: Все сосны – это деревья; Все города – это населенные пункты; Все школы – это учебные заведения; Все тигры – это хищники и т. п.

Другой пример. Возьмем три различных по содержанию высказывания: Если наступает осень, то опадают листья; Если завтра пройдет дождь, то на улице будут лужи; Если вещество – металл, то оно электропроводно. Будучи непохожими друг на друга по содержанию, эти высказывания сходны между собой тем, что строятся по одной и той же форме: Если А, то В. Понятно, что и к этой форме можно подобрать множество содержательных высказываний, например: Если не подготовиться к контрольной работе, то можно получить двойку; Если взлетная полоса покрыта льдом, то самолеты не смогут взлететь; Если слово стоит в начале предложения, то его надо писать с большой буквы и т. п.

Логика не интересуется содержанием мышления (им занимаются другие науки), она изучает только формы мышления; ее интересует не то, что мы мыслим, а то, как мы мыслим, поэтому она часто называется формальной логикой. Например, если по содержанию высказывание Все комары – это насекомые является нормальным, а высказывание Все Чебурашки – это инопланетяне – абсурдным, то для логики эти два высказывания равноценны, так как она занимается формами мышления, а форма у этих высказываний одна и та же: Все А – это В.

Как видим, форма мышления – это способ выражения мыслей, или схема их построения. Существует три формы мышления: понятие, суждение и умозаключение.

Понятие – это форма мышления, которая обозначает какой-либо объект или признак объекта. Примеры понятий: карандаш, растение, небесное тело, химический элемент, мужество, глупость, нерадивость.

Суждение – это форма мышления, которая состоит из понятий, связанных между собой, и что-либо утверждает или отрицает. Примеры суждений: Все планеты являются небесными телами, Некоторые школьники – это двоечники, Все треугольники не являются квадратами.

Умозаключение – это форма мышления, в которой из двух или нескольких исходных суждений (посылок) вытекает новое суждение (вывод).

В логике принято располагать посылки и вывод друг под другом и отделять вывод от посылок (в книге это сделано с помощью знака =>).

Примеры умозаключений:

Все планеты движутся.

Юпитер – это планета.

=> Юпитер движется.

Железо электропроводно.

Медь электропроводна.

Ртуть электропроводна.

Железо, медь, ртуть – металлы.

=> Все металлы электропроводны.

Весь бесконечный мир наших мыслей выражается в понятиях, суждениях и умозаключениях. Об этих трех формах мышления и пойдет речь на страницах книги.

Помимо форм мышления логика также занимается законами мышления. Законы мышления – это такие объективные (т. е. сами по себе существующие и не зависящие от наших желаний и предпочтений) принципы или правила мышления, соблюдение которых всегда приводит рассуждение (независимо от его содержания) к истинным выводам при условии истинности исходных суждений. Основных законов мышления (или законов логики) четыре: закон тождества, закон противоречия, закон исключенного третьего и закон достаточного основания. Подробно каждый из них будет рассмотрен после изучения форм мышления. Нарушение этих законов приводит к различным логическим ошибкам, как правило, к ложным выводам. Иногда законы логики нарушают непроизвольно, по незнанию, но иногда это делают преднамеренно, с целью запутать собеседника и доказать ему какую-нибудь ложную мысль. Такие преднамеренные нарушения логических законов для внешне правильного доказательства ложных мыслей называются софизмами.

Одного здравого смысла и жизненного опыта часто бывает достаточно для решения каких-либо задач. Например, любой человек, не знакомый с логикой, сможет найти подвох в следующем рассуждении:

Движение вечно.

Хождение в школу – это движение.

=> Хождение в школу вечно.

Ложный вывод получается из-за употребления слова движение в разных значениях: в первом суждении оно употребляется в широком, философском смысле, а во втором – в узком, механическом. Однако найти ошибку в рассуждении не всегда просто. Рассмотрим такой пример:

Все мои друзья знают английский язык.

Нынешний президент Америки знает английский язык.

=> Нынешний президент Америки – мой друг.

Понятно, что в этом рассуждении что-то не так. Но что именно? Тот, кто знаком с логикой, скажет, что в данном случае допущена ошибка, которая называется «нераспределенность среднего термина в простом силлогизме». Пусть вас не пугает это незнакомое и на первый взгляд, сложное выражение: в процессе дальнейшего чтения книги вы убедитесь, что ничего сложного, а тем более непонятного здесь нет.

Или такой пример:

Во всех городах за Полярным кругом бывают белые ночи.

Санкт-Петербург не лежит за Полярным кругом.

=> В Санкт-Петербурге не бывает белых ночей.

Как видим, из двух истинных суждений вытекает ложный вывод. В этом рассуждении тоже есть ошибка. Вряд ли не знакомый с логикой человек сможет сразу же ее найти. А тот, кто владеет логической культурой, немедленно установит причину: «расширение большего термина в простом силлогизме». Не пугайтесь: в скором времени мы узнаем, что это такое.

Итак, здравого смысла и жизненного опыта, как правило, достаточно для того, чтобы ориентироваться в различных затруднительных ситуациях. Но если к нашему здравому смыслу и жизненному опыту добавить еще и логическую культуру, то мы от этого только выиграем. Конечно, всех проблем логика не решит, но помочь в жизни она, несомненно, может.

Понятие

Имена вещей (Что такое понятие)

В окружающем нас мире существует бесконечное множество различных объектов и свойств, а в нашем сознании они отражаются в виде понятий.

Понятие – это форма мышления, которая обозначает какой-либо объект или его свойство. Например, один объект мы называем горой, другой – небесным телом, третий – растением; одно свойство или признак мы называем мужеством, другой – хитростью. В языке любое понятие выражается в слове или словосочетании, например: дом, осенний лист, первый президент Америки. Здесь может показаться, что понятие и слово – это одно и то же: например, понятие человек выражается в слове человек. Однако понятие и слово – это разные вещи. Понятие – это мысленное обозначение объекта (мысль о нем), а слово – языковое выражение этой мысли. Понятие – форма мышления, а слово – форма языка. Лучше всего это можно уяснить на примере. Понятие человек для представителей всех народов и национальностей – одно и то же: мысленное отражение или обозначение именно человека, а не растения, небесного тела, геометрической фигуры или молекулы. Но понятие человек в разных языках будет выражаться совершенно разными словами.

Каждое понятие имеет содержание и объем.

Содержание понятия – это наиболее важный признак (или признаки) того объекта, который обозначен

(выражен) этим понятием. Например, чтобы установить содержание понятия человек надо указать такой признак, который является наиболее важным для человека, который отличает его от всех других существ, объектов и предметов. Такой признак для человека – наличие разума. Следовательно, в содержание понятия человек входит только один важный признак – наличие разума. А в содержание понятия мужчина входит уже два важных признака: наличие разума (этот признак повторяется, потому что любой мужчина – это человек) и принадлежность к определенному полу (к одной из половин человечества; слово пол происходит от слова половина). А если надо установить содержание понятия русский мужчина, то следует указать три важных признака: наличие разума, принадлежность к определенному полу и принадлежность к определенной национальности. Таким образом, содержание понятия может включать в себя как один признак какого-либо объекта (или объектов), так и два или более признаков, причем их число зависит от объекта, который обозначается данным понятием. Но почему в одном случае содержание понятия состоит из единственного признака, а в другом – из множества признаков? На этот вопрос ответить несложно, если знать, что такое объем понятия.

Объем понятия – это количество объектов, охватываемых этим понятием, входящих в него. Например, объем понятия человек гораздо больше, чем объем понятия мужчина, потому что мужчин меньше, чем людей вообще. А объем понятия русский мужчина гораздо меньше, чем объем понятия мужчина, потому что русских мужчин на свете намного меньше, чем вообще всех мужчин. И, наконец, объем понятия первый президент России равен единице, потому что включает в себя только одного человека. Точно так же объем понятия город очень широкий, поскольку это понятие охватывает все города в мире, а объем понятия столица меньше объема понятия город, ведь столиц намного меньше, чем городов.

Объем же понятия нынешняя столица России равен единице, потому что включает в себя один-единственный город.

Давайте еще раз вернемся к содержанию и объему понятия и вспомним приведенные выше примеры. Какое понятие – человек или мужчина – больше по содержанию? Конечно же, понятие мужчина, потому что его содержание включает в себя два признака: наличие разума и принадлежность к определенному полу, а в содержание понятия человек входит только один признак: наличие разума. А теперь ответим на вопрос: какое понятие – человек или мужчина – больше по объему? Понятие человек больше, потому что оно охватывает гораздо больше объектов, чем понятие мужчина. Таким образом, между объемом и содержанием понятия существует обратное отношение: чем больше содержание понятия, тем меньше его объем, и наоборот. Например, содержание понятия небесное тело является узким, так как включает в себя только один признак – нахождение вне пределов Земли, однако по объему это понятие очень широкое, потому что оно охватывает огромное количество объектов: любая звезда, планета, метеорит, комета – это небесное тело. А понятие Солнце, наоборот, очень узкое по объему, так как включает только один объект, но очень широкое, богатое по содержанию, которое складывается из множества признаков: размер Солнца, его масса, плотность, химический состав, температура, возраст и т. д.

Все понятия по объему и содержанию делятся на несколько видов. По объему они бывают единичными (в объем входит только один объект, например: Солнце, город Москва, первый президент России, писатель Лев Толстой), общими (в объем входит много объектов, например: небесное тело, город, президент, писатель) и нулевыми (в объем не входит ни одного объекта, например: Баба-яга, Кощей Бессмертный, Дед Мороз, вечный двигатель, марсианский житель, т. е. понятие существует, а объект, который оно обозначает, не существует). По объему понятия также бывают собирательными (обозначают объекты, которые состоят, собираются из какого-то ограниченного набора элементов, делятся, распадаются на какие-то составные части, например: рота солдат, музыкальный коллектив, волчья стая, созвездие) и несобирательными (обозначают объекты, которые не собираются из какого-то ограниченного набора элементов, не делятся на какие-то составные части, являясь чем-то единым, целым, например: человек, растение, звезда, океан, карандаш).

По содержанию понятия бывают конкретными (обозначают какой-либо объект, например: стол, гора, дерево, планета) и абстрактными (обозначают не объект, а признак, свойство, например: мужество, глупость, неряшливость, темнота). По содержанию понятия также бывают положительными (обозначают наличие чего-либо, например: животное, школа, правда, тактичность) и отрицательными (обозначают отсутствие чего-либо, например: не животное, не школа, неправда, бестактность). Легко заметить, что понятие является отрицательным, когда слово, которым оно выражено, употребляется с частицей не или с приставкой без-. Однако если частица не входит в состав слова, которое без нее не употребляется (например: неряха, неряшливость, ненастье, нерадивость, невежество), то понятие, выраженное таким словом, будет положительным.

Любому понятию можно дать логическую характеристику, т. е. разобрать его по объему и содержанию. Сначала надо определить, единичным, общим или нулевым оно является, потом установить, собирательное оно или несобирательное, затем выяснить, конкретное оно или абстрактное, и, наконец, ответить на вопрос – положительное оно или отрицательное.

Например, понятие Солнце – единичное (потому что в его объем входит только один объект, одно небесное тело), несобирательное (так как Солнце не состоит ни из каких частей, не делится на них), конкретное (ведь Солнце это объект, а не признак или свойство), положительное (потому что этим понятием обозначается наличие, а не отсутствие объекта). Точно так же растение – это понятие общее, несобирательное, конкретное и положительное, а понятие созвездие Ориона – единичное, собирательное, конкретное и положительное.

Молодой человек и вредная привычка (Определенные и неопределенные понятия)

Понятие является определенным, когда оно имеет ясное содержание и резкий объем. Как мы уже знаем, содержание понятия – это наиболее важные признаки того объекта, который оно выражает, а объем – это количество охватываемых им объектов. Таким образом, понятие имеет ясное содержание в том случае, если можно точно указать набор существенных признаков выражаемого объекта, а также точно установить границу между теми объектами, которые это понятие охватывает, и теми, которые не принадлежат к его объему. Например, понятие мастер спорта является определенным. Оно имеет ясное содержание, так как можно точно указать его наиболее важный отличительный признак – официально обладать спортивным разрядом мастера спорта. Это понятие имеет резкий объем – относительно любого человека можно точно сказать, является он мастером спорта или нет, т. е. попадает или не попадает в объем данного понятия; иначе говоря, можно провести границу между всеми мастерами спорта и всеми, кто ими не является, точно отделить одних от других.

Понятие является неопределенным, когда оно имеет неясное содержание и нерезкий объем. Понятие характеризуется неясным содержанием, если невозможно точно указать наиболее важные отличительные признаки того объекта, который оно выражает; а нерезкий объем понятия свидетельствует о невозможности провести точную границу между теми объектами, которые входят в объем этого понятия, и теми, которые не входят в него. Например, понятие хороший спортсмен является неопределенным. Оно имеет неясное содержание, так как невозможно с точностью указать существенные признаки хорошего спортсмена, ведь нельзя однозначно ответить на вопрос, кого следует считать хорошим спортсменом. То ли это тот, кто имеет разряд не ниже мастера спорта, то ли тот, кто установил не менее одного мирового рекорда, то ли многократный олимпийский чемпион, то ли тот, кто сам себя таковым считает. Понятно, что и мнения разных людей по поводу того, кого надо относить к хорошим спортсменам, будут различаться: одни будут утверждать одно, другие – другое. Также это понятие имеет нерезкий объем – относительно любого человека невозможно точно сказать, является он хорошим спортсменом или нет, т. е. попадает или не попадает в объем данного понятия; иначе говоря, нельзя провести границу между множеством хороших спортсменов и всеми, кто ими не является.

Объем и содержание понятия, как уже говорилось, тесно связаны друг с другом. Однако если в количественном отношении связь между ними обратная (чем больше объем понятия, тем меньше его содержание, и наоборот), то в качественном отношении эта связь прямая: ясное содержание понятия обусловливает его резкий объем, а неясному содержанию обязательно соответствует нерезкий объем.

Конечно, намного удобнее и проще обращаться с определенными понятиями, чем с неопределенными, однако последние также весьма важны и часто употребляются в мышлении и языке. Основных причин появления и существования неопределенных понятий несколько.

Во-первых, многие объекты, свойства и явления окружающего мира многогранны и сложны. Они-то, как правило, и выражаются в мышлении неопределенными понятиями. Например, понятие любовь, отличаясь в высшей степени неясным содержанием и, соответственно, нерезким объемом, является неопределенным: оно обозначает явление настолько сложное, что за всю историю человечества никто так и не смог окончательно и исчерпывающе ответить на вопрос о том, что же такое любовь.

Во-вторых, как верно заметили еще древние греки, все в мире постоянно меняется. Многообразие и плавность переходов из одного состояния в другое трудно выразить точно и однозначно, в виде определенных понятий. Неудивительно, что эти переходы обычно обозначаются неопределенными понятиями. Можем ли мы точно сказать, когда человек является юным, когда молодым, когда зрелым, когда он достигает средних лет и, наконец, когда становится старым? Разумеется, понятия юный, молодой, зрелый, старый и многие другие, им подобные, являются неопределенными.

В-третьих, существование неопределенных понятий во многом связано с тем, что люди зачастую по-разному оценивают одни и те же объекты, свойства, явления и события. Одному человеку некая книга покажется интересной, другому – скучной. Какой-то поступок может у одного вызвать восхищение, у другого – негодование, а третьего оставит равнодушным. Различия в оценках окружающей нас действительности воплощаются в неопределенности многих понятий, например: интересный фильм, модная одежда, способный ученик, скучная книга, трудная задача, недостойное поведение, симпатичная девушка, вкусное блюдо.

Названные причины появления и существования неопределенных понятий тесно связаны между собой. Они действуют всегда сообща, и, скорее всего, в любом неопределенном понятии можно усмотреть одновременное участие этих причин.

Несмотря на неясность содержания и нерезкость объема неопределенных понятий, мы обычно пользуемся ими без особенных затруднений, как правило, интуитивно понимая, о чем идет речь, когда говорят о скучной книге, неинтересном фильме, умном человеке, бессовестной выходке, удобном кресле, высокой зарплате и т. п. Конечно же, если бы в мышлении и языке функционировали только определенные понятия, то они (мышление и язык) были бы более точными. Тогда исчезли бы разночтения, двусмысленность, неясность, в человеческом общении стало бы намного меньше взаимного непонимания и разногласий. Однако большая точность мышления и языка сделала бы их более бедными и менее выразительными. В одном из учебников по логике^[1] предлагается вспомнить описание Чичикова из «Мертвых душ» Н. В. Гоголя: В бричке сидел господин не красавец, но и не дурной наружности, не слишком толст, не слишком тонок; нельзя сказать, чтобы стар, однако ж и не так чтобы слишком молод.

Описание внешности героя целиком состоит из неопределенных понятий. Но ведь можно было бы составить это описание и из определенных понятий. Тогда оно выглядело бы, например, так: В бричке сидел господин 45 лет, ростом 175 см, в ботинках 41 размера, окружность головы – 60 см, объем груди – 80 см…

Однако в данном случае перед нами было бы не художественное произведение, а что-то вроде милицейского протокола.

В некоторых областях мышления и языка невозможно обойтись без неопределенных понятий. Но и в повседневном общении часто более уместны неопределенные понятия, чем определенные. Скорее всего, мы скажем, характеризуя кого-то, просто высокий человек, а не человек ростом 187 см. Стремясь сделать мышление и язык более точными, пытаясь изгнать из них неопределенные понятия, мы рискуем остаться вообще без мышления и языка. Натачивая лезвие ножа, пытаясь достичь его максимальной остроты, можно точить его до тех пор, пока от лезвия ничего не останется.

Итак, неопределенные понятия занимают значительное место в нашей интеллектуально-речевой практике. Они представляют собой ее неотъемлемый компонент, и избавление от них так же лишено смысла, как и невозможно. Неопределенные понятия являются источником неточности, разногласий и коммуникативных (связанных с общением) помех не сами по себе, а в зависимости от той ситуации, в которой они употребляются. Как уже говорилось, в художественной литературе они даже необходимы. К различного рода трудностям неопределенные понятия могут привести, если они употребляются, например, в официальных документах. Неопределенные понятия, попавшие в тексты законов, могут создать основу для разночтений и неверных решений. Так, понятие нарушение общественного порядка является неопределенным и, присутствуя в тексте какого-либо законодательного акта без поясняющих комментариев, может стать причиной оправдания виновного и наказания невиновного.

Неопределенные понятия нежелательны не только в законах, но и в других текстах, которые имеют отношение к официально-деловой сфере. Это инструкции, анкеты, договоры и т. п.

Например, хорошо известна ситуация, когда зарубежный производитель предметов бытовой техники пишет в инструкции к своим изделиям смехотворные рекомендации, вроде Не использовать микроволновую печь для просушки домашних животных. Кажется, что достаточно было бы сказать: Не использовать изделие не по назначению. Мы смеемся над пресловутой глупостью иностранцев, которых надо специально предупреждать, чтобы они не сушили своих питомцев после купания в микроволновой печке. На самом деле, они совсем не глупы, а, напротив, достаточно хитры.

Понятие использование изделия не по назначению является неопределенным и вполне может стать основой для судебного иска к производителю предметов бытовой техники.

Представьте себе, что некий предприимчивый пользователь, внимательно прочитав инструкцию, преднамеренно просушил в микроволновой печке кошку, которая от этой сушки сдохла, после чего подал судебный иск на компанию-производителя, мотивируя его тем, что использование изделия не по назначению не предполагает невозможность сушить в нем домашних животных, а, следовательно, в гибели кошки виновата компания, которая не предупредила пользователя и поэтому должна пострадавшему немалую сумму в качестве компенсации морального ущерба.

Казалось бы, подобные иски невозможны, поскольку в любом суде они не вызовут ничего, кроме крайнего недоумения. Однако в Америке они всерьез рассматриваются и по ним действительно выплачиваются компенсации. Поэтому если в инструкции к бытовому прибору появился пункт, запрещающий сушить в микроволновке домашних животных, значит, какой-то хитрый гражданин создал судебный прецедент и выиграл дело; после чего производитель и поменял в инструкции к своему изделию неопределенное понятие на определенное.

Все писатели – люди, но не все люди – писатели (Отношения между понятиями)

Понятия бывают совместимыми и несовместимыми.

Совместимыми называются понятия, объемы которых имеют общие элементы, каким-либо образом соприкасаются. Например, понятия спортсмен и американец совместимые, так как их объемы имеют общие элементы или объекты: есть такие спортсмены, которые являются американцами, и наоборот, есть такие американцы, которые являются спортсменами.

Несовместимыми называются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Например, понятия треугольник и квадрат являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом, и наоборот.

Совместимые понятия могут находиться в отношениях равнозначности, пересечения и подчинения.

Понятия находятся в отношении равнозначности в том случае, если их объемы полностью совпадают. Например, равнозначными будут понятия квадрат и равносторонний прямоугольник, ведь любой квадрат – это равносторонний прямоугольник, а любой равносторонний прямоугольник – это квадрат.

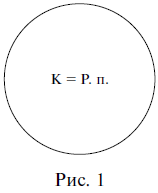
В логике отношения между понятиями принято изображать с помощью круговых схем Эйлера^[2]. Объемы понятий на них изображаются отдельными кругами. Взаимное расположение кругов на схеме показывает то или иное отношение между понятиями: они могут полностью совпадать, или пересекаться, или не соприкасаться, или один круг может располагаться внутри другого. Так, отношение равнозначности между понятиями квадрат (К) и равносторонний прямоугольник (Р. п.) изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают (рис. 1).

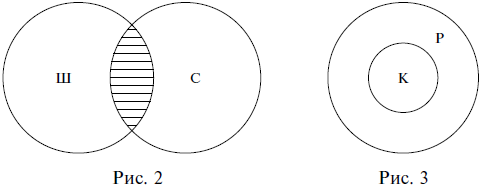
Понятия находятся в отношении пересечения, когда их объемы совпадают только частично. Например, пересекающимися будут понятия школьник (Ш) и спортсмен (С): есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (рис. 2). Заштрихованная часть показывает частично совпадающие объемы двух понятий.

Понятия находятся в отношении подчинения, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия карась (К) и рыба (Р), так как все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим – родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого (рис. 3).

Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.

Несовместимые понятия могут находиться в отношениях соподчинения, противоположности и противоречия.

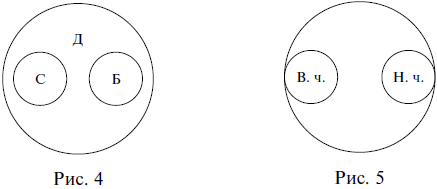
Понятия находятся в отношении соподчинения, когда их объемы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия сосна (С) и береза (Б) являются соподчиненными: ни одна сосна не может быть березой, и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дерево (Д). На схеме Эйлера отношение соподчинения изображается несоприкасающимися кругами (рис. 4).

Понятия находятся в отношении противоположности, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия высокий человек (В. ч.) и низкий человек (Н. ч.) Третьим (переходным) вариантом между ними будет понятие человек среднего роста. На схеме Эйлера отношение противоположности изображается двумя несоприкасающимися кругами, которые находятся как бы на разных полюсах (рис. 5).

Поскольку объемы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью березы, а береза – противоположностью сосны: это просто разные деревья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека, и наоборот. Так же противоположными будут понятия темная комната и светлая комната, горячая вода и холодная вода, белый лист и черный лист, глубокая речка и мелкая речка и т. п.

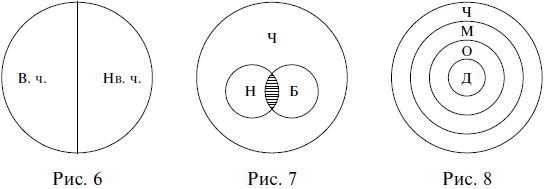
Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий между противоречащими понятиями не может быть третьего (среднего) варианта. Например, в отношении противоречия находятся понятия высокий человек (В. ч.) и невысокий человек (Нв. ч.). В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и низкий человек, и человек среднего роста – это невысокий человек. На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия (рис. 6).

Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.

Итак, в логике выделяется шесть вариантов отношений между понятиями. Любые два понятия обязательно находятся в одном из шести указанных случаев отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Санкт-Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д.

Если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом, находятся в отношении соподчинения, поскольку часть и целое – не то же самое, что вид и род.

До сих пор круговыми схемами Эйлера мы изображали в основном отношения между двумя понятиями, но это можно сделать для большего числа понятий. Например, отношения между понятиями боксер (Б), негр (Н) и человек (Ч) изображаются следующей схемой Эйлера (рис. 7).

Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения: боксер может быть негром и может им не быть, а негр также может быть боксером и может им не быть, а понятия боксер и человек, так же как понятия негр и человек, находятся в отношении подчинения: любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром.

Рассмотрим отношения между понятиями дедушка (Д), отец (О), мужчина (М), человек (Ч) с помощью схемы Эйлера (рис. 8).

Указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.

От рода к виду и обратно (Ограничение и обобщение понятий)

Видовые и родовые понятия тесно связаны между собой логическими операциями ограничения и обобщения.

Ограничение понятия – это логическая операция перехода от родового понятия к видовому с помощью прибавления к его содержанию какого-либо признака (или нескольких признаков). Вспомним об обратном отношении между объемом и содержанием понятия: чем больше объем, тем меньше содержание, и наоборот. Ограничение понятия, или переход от родового понятия к видовому, – это уменьшение его объема, а значит – увеличение содержания. Вот почему при добавлении каких-либо признаков к содержанию понятия автоматически уменьшается его объем. Например, если к содержанию понятия физический прибор (Ф. п.) прибавить признак измерять напряжение электрического тока, то оно превратится в понятие вольтметр (В), которое будет видовым по отношению к исходному родовому понятию физический прибор (рис. 9).

Если к содержанию понятия геометрическая фигура (Г. ф.) прибавить признак иметь равные стороны и прямые углы, то оно превратится в понятие квадрат (К), которое будет видовым по отношению к исходному родовому понятию геометрическая фигура (рис. 10).

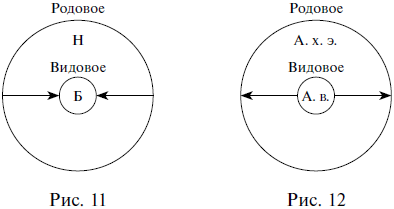
Обобщение понятия – это логическая операция перехода от видового понятия к родовому с помощью исключения из его содержания какого-либо признака (или нескольких признаков). Содержание понятия, лишенное каких-то признаков, уменьшается, но при этом автоматически увеличивается объем понятия, которое из видового становится родовым или обобщается. Например, если от содержания понятия биология (Б) отбросить признак изучать различные формы жизни, то оно превратится в понятие наука (Н), которое будет родовым по отношению к исходному видовому понятию биология (рис. 11).

Если от содержания понятия атом водорода (А. в.) отбросить признак иметь один электрон, то оно превратится в понятие атом химического элемента (А. х. э.), которое будет родовым по отношению к исходному видовому понятию атом водорода (рис. 12).

Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие Солнце, то получится следующая цепочка: Солнце → звезда → небесное тело → физическое тело → форма материи. В этой цепочке понятие звезда является родовым по отношению к понятию Солнце, но видовым по отношению к понятию небесное тело; так же понятие небесное тело является родовым по отношению к понятию звезда, но видовым по отношению к понятию физическое тело, и т. д. Движение по нашей цепочке от понятия Солнце к понятию форма материи представляет собой серию последовательных обобщений, а движение в обратном направлении – серию ограничений. Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький будет соответствовать понятию Солнце, а самый большой – понятию форма материи.

Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие, а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие, например: объект мироздания, форма материи или форма бытия.

Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некоего целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части. Например, в качестве ограничения понятия цветок предлагают понятие стебель. Действительно, стебель – это часть цветка, но ограничить понятие – значит подобрать не часть для целого, а вид для рода. Следовательно, правильным ограничением понятия цветок будет понятие ромашка, или тюльпан, или хризантема и т. п. В качестве обобщения понятия дерево нередко предлагают понятие лес. Конечно же, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить понятие – значит подобрать не целое для части, а род для вида. Следовательно, правильным обобщением понятия дерево будет понятие растение, или объект флоры, или живой организм и т. п.

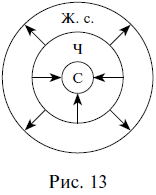
Итак, почти любое понятие (за исключением единичных и широких, философских) можно как ограничить, так и обобщить. Другими словами, подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия человек (Ч) будет понятие спортсмен (С) или писатель, или мужчина, или молодой человек и т. п., а его обобщением будет понятие живое существо (Ж. с.) (рис. 13).

Лев – это царь зверей (Определение понятия)

Определение понятия – это логическая операция, которая раскрывает содержание понятия. Определения бывают явными и неявными.

Явное определение непосредственно раскрывает содержание понятия, дает прямой ответ на вопрос, чем является объект, который оно обозначает. Например: Термометр – это физический прибор, предназначенный для измерения температуры – явное определение.

Неявное определение раскрывает содержание понятия не прямо, а косвенно, с помощью контекста, в котором это понятие употребляется. Например, из фразы: Во время этого грандиозного эксперимента сверхточные термометры зафиксировали температуру в 1000 °С – косвенно следует ответ на вопрос: Что такое термометр? – т. е. вытекает неявное определение этого понятия. Понятно, что определениями в полном смысле этого слова надо считать явные определения. В дальнейшем речь пойдет именно о них.

Определения бывают реальными и номинальными.

Реальное определение раскрывает содержание понятия, обозначающего какой-то объект, т. е. оно отнесено к объекту. Например: Термометр – это физический прибор, предназначенный для измерения температуры, – реальное определение.

Номинальное определение (от лат. nomen – «имя») раскрывает значение термина, которым выражено какое-либо понятие, т. е. оно отнесено к термину (слову).

Например: Слово «термометр» обозначает физический прибор, предназначенный для измерения температуры, – номинальное определение.

Как видим, принципиальной разницы между реальными и номинальными определениями не существует. Они различаются, как правило, по форме, но не по сути.

Существует несколько способов определения понятия, но среди них особо выделяется классический способ – когда определяемое понятие подводится под ближайшее к нему родовое понятие, после чего следует указание на его видовое отличие. Например, определение: Астрономия – это наука о небесных телах построено по классическому способу. В нем определяемое понятие астрономия сначала подводится под ближайшее к нему родовое понятие наука (астрономия – это обязательно наука, но наука – это не обязательно астрономия), а потом указывается на видовое отличие астрономии от других наук: о небесных телах. Фактически все определения, встречающиеся в научной, учебной и справочной литературе, например в толковых словарях, построены по классическому способу.

Пользуясь классическим способом, вы сможете дать точное и правильное определение любому понятию, конечно, если определяемый объект или термин вам хорошо знаком и вы знаете, что он собой представляет или что означает соответственно. Например, требуется дать определение понятию квадрат. Следуя классическому способу, сначала подведем его под родовое понятие: Квадрат – это геометрическая фигура, – а затем укажем его видовое отличие от других геометрических фигур, которое заключается в наличии равных сторон и прямых углов. Получаем определение: Квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые.

Давая определение понятию квадрат, мы могли бы подвести его под более близкое родовое понятие прямоугольник, и тогда определение получилось бы следующим: Квадрат – это прямоугольник, у которого все стороны равны.

Однако верно и приведенное выше определение квадрата, которое также раскрывает содержание соответствующего понятия.

Существует несколько логических правил составления определений. Нарушение хотя бы одного из них приводит к тому, что содержание понятия не будет раскрыто и определение станет неверным. Рассмотрим эти правила.

1. Определение не должно быть широким, т. е. определение не должно превышать своим объемом определяемое понятие. Например, определение Солнце – это небесное тело является широким, так как определение небесное тело по объему намного больше определяемого понятия Солнце. Из приведенного определения не вполне понятно, что такое Солнце, ведь небесное тело – это и планета, и комета и т. п. В данном случае можно также сказать, что, пользуясь классическим способом определения, мы подвели определяемое понятие Солнце под родовое понятие небесное тело, но не сделали второй шаг – не указали на видовое отличие.

Примеры широких определений:

• Лошадь – это млекопитающее позвоночное животное.

• Кость – это орган, обладающий сложным строением.

• Барометр – это метеорологический измерительный прибор.

2. Определение не должно быть узким, т. е. определение не должно быть по своему объему меньше определяемого понятия. Например, определение Геометрия – это наука о треугольниках является узким. Геометрия – действительно наука о треугольниках, но не только о них, а в нашем примере определение получилось по объему меньше определяемого понятия, в результате чего из него не совсем ясно, что такое геометрия, содержание понятия не раскрывается.

Примеры узких определений:

Птица – это животное, имеющее крылья и умеющее летать.

• Революция – это крупное историческое событие, в результате которого в обществе меняется политическая власть.

• Феодализм – это общественный строй, основанный на эксплуатации.

Как видим, ошибка узкого определения противоположна ошибке широкого определения. Если определение не должно быть широким и не должно быть узким, то каким же тогда оно должно быть? Оно должно быть соразмерным, т. е. понятие и его определение должны быть равны друг другу. Вернемся к определению Астрономия – это наука о небесных телах, которое является соразмерным. В этом примере определяемое понятие астрономия и определение наука о небесных телах находятся в отношении равнозначности: астрономия – это именно наука о небесных телах, а наука о небесных телах – это только астрономия.

Определение является соразмерным, если между его первой частью (определяемым понятием) и второй (определением) можно поставить знак равенства (=). Если же между первой и второй частью определения ставится знак «меньше» (<) или «больше» (>), то оно является ошибочным – широким или узким соответственно. В данном случае мы видим проявление одного из основных законов логики – закона тождества.

3. В определении не должно быть круга, т. е. в нем нельзя употреблять понятия, которые являются определяемыми. Например, в определении Клеветник – это человек, который занимается клеветой, присутствует круг, поскольку понятие клеветник определяется через понятие клевета, т. е. фактически – через само себя. Если бы, услышав приведенное определение, мы спросили, что такое клевета, нам могли бы ответить: Клевета – это то, чем занимается клеветник. Присутствующий в определении круг, или тавтология (от греч. tauto – «то же самое»; logos – «слово»), приводит к тому, что содержание понятия не раскрывается и определение является ошибочным.

Однако наверняка найдутся люди, которые скажут, что из определения Клеветник – это человек, который занимается клеветой, вполне понятно, и кто такой клеветник, и что такое клевета. Они могут так утверждать только потому, что им ранее было известно значение слов клеветник и клевета. Станет ли понятно, что такое экзистенциализм из следующего кругового определения: Экзистенциализм – это философское направление XX веке, в котором ставятся и всесторонне рассматриваются различные экзистенциальные вопросы и проблемы! Узнаем ли мы, что такое синергетика, благодаря такому круговому определению: Синергетика – это раздел современного естествознания, который изучает разнообразные синергетические явления и процессы!

Примеры определений, в которых есть круг:

• Творческое мышление – это мышление, которое обеспечивает решение творческих задач.

• Фильтрование – это процесс разделения какого-либо вещества с помощью специального приспособления – фильтра.

• Сверхпроводник – это вещество, обнаруживающее явление сверхпроводимости.

4. Определение не должно быть двусмысленным, т. е. в нем нельзя употреблять слова (термины) в переносном значении. Вспомним хорошо знакомое с детства определение Лев – это царь зверей. В данном определении слово царь используется в переносном значении, но у него есть и прямое значение. Получается, что в определении употребляется одно слово, а возможных значений у него два, т. е. определение является двусмысленным (вновь нарушается логический закон тождества: одно слово, два значения: 1 ≠ 2). Двусмысленность вполне уместна в качестве художественного приема, но в определении она недопустима, поскольку содержание понятия в данном случае не раскрывается.

Примеры двусмысленных определений:

Собака – это друг человека (двусмысленное определение).

Математика – это гимнастика ума (двусмысленное определение).

Краткость – это сестра таланта.

5. Определение не должно быть сложным и непонятным. Иначе говоря, оно должно быть коммуникабельным, т. е. понятным для своего адресата – человека, которому оно предназначено. Рассмотрим следующее определение: Энтропия – это термодинамическая функция, характеризующая часть внутренней энергии замкнутой системы, которая не может быть преобразована в механическую работу. Это определение взято не из научного доклада и не из докторской диссертации, а из учебника для студентов гуманитарных специальностей^[3]. Данное определение не широкое и не узкое, в нем нет круга и двусмысленности, оно верно и с научной точки зрения. Это определение кажется безупречным с тем только исключением, что оно является сложным и непонятным, или некоммуникабельным для людей, которые не занимаются специально естественными науками, т. е. для большинства из нас. Определение должно быть понятным для того, кому оно адресовано, иначе при всей своей формальной правильности оно не будет раскрывать содержания понятия для своего адресата.

Примеры некоммуникабельных определений:

Суффикс – это выделяющаяся в составе словоформы послекорневая аффиксальная морфема.

Жизнь – это активный процесс поддержания и самовоспроизведения специфической структуры, происходящий с потреблением энергии, получаемой извне.

6. Определение не должно быть только отрицательным.

Например, определение Квадрат – это не треугольник является только отрицательным. Квадрат – это действительно не треугольник, но данное определение не раскрывает содержание понятия квадрат, ведь, указав на то, чем не является объект, обозначенный определяемым понятием, мы не сказали, чем же он является (окружность, трапеция, пятиугольник – это тоже не квадраты). Определение может быть отрицательным в том случае, когда оно дополнено положительной частью. Например, является правильным определение Квадрат – это не треугольник, а прямоугольник, у которого все стороны равны. Примеры только отрицательных определений:

Извлечение квадратного корня – это математическое действие, которое не является ни умножением, ни делением, ни возведением в степень.

Человек не является ни птицей, ни рыбой.

Транспорт бывает общественным, личным и наземным (Деление понятия)

Деление понятия – это логическая операция, которая раскрывает его объем. Принято выделять делимое понятие, результаты деления и основание деления (признак, по которому производится деление). Например, в делении Люди бывают мужчинами и женщинами (или, что то же самое: Люди делятся на мужчин и женщин) делимым является понятие люди, результаты деления – это понятия мужчины и женщины, а основание деления – пол, так как люди в нем разделены по половому признаку. В зависимости от основания деление может быть различным. Например: Люди бывают высокими, низкими и среднего роста (основание деления – рост); Люди бывают монголоидами, европеоидами и негроидами (основание деления – раса); Люди бывают учителями, врачами, инженерами и т. д. (основание деления – профессия). Иногда понятие делится дихотомически (от греч. dicha – «на две части» и tome – «разрез, сечение») по типу А и не А. Например: Люди бывают спортсменами и не спортсменами. Дихотомическое деление всегда правильное, т. е. в нем автоматически исключаются все возможные в делении ошибки, о которых речь пойдет ниже.

Мы хорошо знаем, зачем нам нужна операция определения понятия: знакомство с новым предметом начинается с его определения. Теперь ответим на вопрос, какую роль в мышлении и языке выполняет операция деления понятия. Изучая разные науки, вы заметили, что ни одна из них не обходится без различных классификаций: разделений каких-то областей действительности на группы, части, виды и т. п. (классификация растений в ботанике, животных – в зоологии, химических элементов – в химии и т. д.).

Любая классификация – это не что иное, как логическая операция деления понятия. Классификации могут быть как обширными, подробными, научными, так и простыми, обыденными, повседневными. Когда мы говорим: Люди делятся на мужчин и женщин или Учебные заведения бывают начальными, средними и высшими, то создаем пусть маленькую и простую, но классификацию. Итак, логическая операция деления понятия лежит в основе любой классификации, без которой не обходится ни научное, ни повседневное мышление.

Существует несколько логических правил деления. Нарушение хотя бы одного из них приводит к тому, что объем понятия не раскрывается и деление становится неверным. Рассмотрим эти правила.

1. Деление должно проводиться по одному основанию, т. е. при делении понятия следует придерживаться только одного выбранного признака. Например, в делении Люди бывают мужчинами, женщинами и учителями используются два разных основания (пол и профессия), что недопустимо. Ошибка, возникающая при нарушении этого правила, называется подменой основания. В делении с подменой основания могут использоваться не только два разных основания, как в приведенном выше примере, но и больше. Например, в делении Люди бывают мужчинами, женщинами, китайцами и блондинами использованы три разных основания (пол, национальность и цвет волос), что, конечно же, тоже является ошибкой.

Подмена основания присутствует в следующих примерах делений:

• Транспорт бывает наземным, подземным, водным, воздушным, общественным и личным.

• Речь бывает устной, письменной, путаной и заумной.

• Оружие бывает холодным, огнестрельным и старинным.

2. Деление должно быть полным, т. е. надо перечислить все возможные результаты деления (суммарный объем всех результатов деления должен быть равен объему исходного делимого понятия). Например, деление Учебные заведения бывают начальными и средними является неполным, так как не указан еще один результат деления – высшие учебные заведения. Но как быть, если надо перечислять не два или три, а десятки или сотни результатов деления. В этом случае можно употреблять выражения и другие, и прочие, и так далее, и тому подобное, которые будут включать в себя неперечисленные результаты деления. Например: Люди бывают русскими, немцами, китайцами, японцами и представителями других национальностей.

Примеры неполных делений:

Энергия бывает механической и химической.

Треугольники бывают тупоугольными и прямоугольными.

3. Результаты деления не должны пересекаться, т. е. понятия, представляющие собой результаты деления, должны быть несовместимыми, их объемы не должны иметь общих элементов (на схеме Эйлера круги, соответствующие результатам деления, не должны соприкасаться). Например, в делении Страны мира делятся на северные, южные, восточные и западные допущена ошибка – пересечение результатов деления. На первый взгляд, приведенное деление кажется безошибочным: оно проведено по одному основанию (сторона света) и является полным (все стороны света перечислены). Чтобы увидеть ошибку, надо рассуждать так. Возьмем какую-нибудь страну, например Канаду, и ответим на вопрос, является ли она северной. Конечно, является, так как расположена в северном полушарии Земли. А является ли Канада западной страной? Да, потому что она расположена в западном полушарии. Таким образом, получается, что Канада – одновременно и северная, и западная страна, т. е. она является общим элементом объемов понятий северные страны (С) и западные страны (3), а значит, эти понятия пересекаются. То же самое можно сказать и относительно понятий южные страны (Ю) и восточные страны (В). На схеме Эйлера результаты деления из нашего примера будут располагаться так (рис. 14).

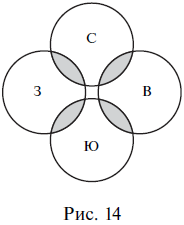
Вспомним, каждая классификация построена таким образом, что любой элемент, попадающий в одну ее группу (часть, вид), ни в коем случае не попадает в другие. Это и есть следствие непересечения результатов деления (их взаимоисключения).

Примеры делений с пересечением результатов:

Художественные романы бывают приключенческими, детективными, фантастическими, историческими, любовными и другими.

Спортивные состязания бывают мировыми, международными, олимпийскими и другими.

По темпераменту люди делятся на сангвиников, меланхоликов, флегматиков и холериков.

4. Деление должно быть последовательным, т. е. не допускающим пропусков и скачков. Рассмотрим следующее деление: Леса бывают хвойными, лиственными, смешанными и сосновыми. Явно лишним здесь выглядит понятие сосновые леса, в силу чего допущенная в делении ошибка напоминает подмену основания. Однако основание в данном случае не менялось: деление было проведено по одному и тому же основанию – тип древесных листьев. Правильно было бы разделить леса на хвойные, лиственные и смешанные, а потом произвести второе деление – разделить хвойные леса на сосновые и еловые. Таким образом, надо было совершить два последовательных деления, а в приведенном примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении. Еще раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении Учебные заведения бывают начальными, средними, высшими и университетами присутствует скачок, а в делении Учебные заведения бывают начальными, средними, высшими и коммерческими допущена подмена основания.

Примеры делений, в которых присутствует скачок:

Геометрические фигуры делятся на плоские, объемные, треугольники и квадраты.

Учащиеся бывают успевающими, отстающими и отличниками.

Преступления делятся на умышленные, неумышленные и квартирные кражи.

Либо школьник, либо спортсмен (Сложение и умножение понятий)

Помимо рассмотренных нами логических операций ограничения, обобщения, определения и деления понятия, существуют еще две важные операции. Это сложение и умножение понятий.

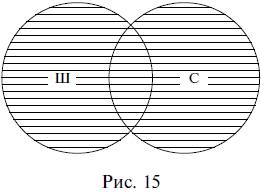
Сложение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой (рис. 15).

Умножение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (рис. 16).

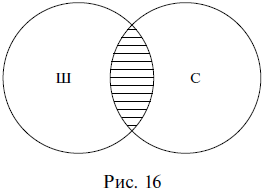
Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения: школьник и спортсмен. При других отношениях между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично совпадают в пересечении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а результатом умножения – видовое.

Как правило, в естественном языке (том, на котором мы общаемся) результат сложения понятий выражается союзом ИЛИ, а умножения – союзом И. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является ИЛИ школьником, ИЛИ спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является И школьником, И спортсменом одновременно.

О возможных разночтениях при употреблении союзов ИЛИ и ИВ. И. Свинцов^[4] пишет: «Что касается союзов ИЛИ и И, то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: Безбилетный проезд и бесплатный провоз багажа наказываются штрафом! Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билеты, в другое – не оплатившие провоз багажа.

Если союз И рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза ИЛИ здесь следует признать предпочтительным».

Однако следует отметить, что и в данном случае из-за неоднозначности разделительного союза ИЛИ могут возникнуть недоразумения. Дело в том, что этот союз может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании Можно изучать английский язык или немецкий союз ИЛИ употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другого не исключает. В данном случае разделительный союз ИЛИ очень близок к соединительному союзу И. С другой стороны, в высказывании Он родился в 1987 году или в 1989 году союз ИЛИ употребляется в строгом значении, так как если он родился в 1987 году, то никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза ИЛИ мы еще будем говорить далее.)

Если в рассмотренное выше правило пользования городским транспортом поставить союз ИЛИ вместо союза И, как предлагает В. И. Свинцов, то получится следующее: Безбилетный проезд или бесплатный провоз багажа наказываются штрафом. В данном случае союз ИЛИ, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.

В силу всего сказанного надо отметить, что употребление союза ИЛИ всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны различного рода недоразумения. Поэтому нередко употребляется своеобразный союз-гибрид ИЛИ/И, указывающий на то, что союз ИЛИ используется в некоем тексте в его нестрогом значении. Таким образом, наиболее целесообразно сформулировать правило оплаты проезда в городском пассажирском транспорте следующим образом: Безбилетный проезд или/и бесплатный провоз багажа наказываются штрафом. В данной, может быть, не совсем удобной, с точки зрения языка, формулировке все возможные разночтения и недоразумения исключаются.

Суждение

Параллельные прямые не пересекаются (Что такое суждение)

Суждение (высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например: Все сосны являются деревьями, Некоторые люди – это спортсмены, Ни один кит – не рыба, Некоторые животные не являются хищниками. Рассмотрим несколько важных свойств суждения, которые в то же время отличают его от понятия.

1. Любое суждение состоит из понятий, связанных между собой. Например, если связать понятия карась и рыба, то могут получиться суждения Все караси являются рыбами, Некоторые рыбы являются карасями.

2. Любое суждение выражается в форме предложения (как мы помним, понятие выражается словом или словосочетанием). Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда что-либо утверждает или отрицает, в силу чего суждение выражается в форме повествовательного предложения.

Тем не менее есть такие вопросительные и восклицательные предложения, которые только по форме являются вопросами и восклицаниями, а по смыслу что-то утверждают или отрицают. Они называются риторическими. Например, известное высказывание И какой же русский не любит быстрой езды? представляет собой риторическое вопросительное предложение (риторический вопрос), так как в нем в форме вопроса утверждается, что всякий русский любит быструю езду. В подобном вопросе заключено суждение. То же самое можно сказать о риторических восклицаниях. Например, в высказывании Попробуй найти черную кошку в темной комнате, если ее там нет! в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение. Понятно, что не риторический, а настоящий вопрос (например: Как тебя зовут?) не выражает суждение, точно так же, как не выражает его настоящее, а не риторическое восклицание (например: Прощай, свободная стихия!).

Чтобы лучше уяснить, что такое суждение, рассмотрим несколько примеров.

• Неужели ты не знал, что Земля вращается вокруг Солнца? (Риторический вопрос – является суждением).

• Прощай, немытая Россия! (Восклицание – суждением не является).

• Кто написал философский трактат «Критика чистого разума»? (Вопрос – суждением не является).

• Логика появилась примерно в V в. до н. э. в Древней Греции. (Повествование – является суждением).

• Первый президент Америки. (Понятие – суждением не является).

• Разворачивайтесь в марше! (Восклицание – суждением не является).

• Мы все учились понемногу… (Повествование – является суждением).

• Попробуй-ка двигаться со скоростью света! (Риторическое восклицание – является суждением).

• Средняя школа № 469 г. Москвы. (Понятие – суждением не является).

• Как тебе только не стыдно? (Риторический вопрос – является суждением).

• Каким образом решается знаменитая задача о квадратуре круга? (Вопрос – суждением не является).

• Общая теория относительности А. Эйнштейна. (Понятие – суждением не является).

• Почему нельзя делить на ноль? (Вопрос – суждением не является).

• Бескрайние просторы Вселенной. (Понятие – суждением не является).

• Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. (Повествование – является суждением).

3. Любое суждение является истинным или ложным.

Если суждение соответствует действительности, оно истинное, а если не соответствует – ложное. Например, суждение Все розы – это цветы является истинным, а суждение Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа – истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета – ложное и т. п. Но разве понятия Змей Горыныч, Кощей Бессмертный, вечный двигатель не ложные? Нет, эти понятия являются нулевыми (пустыми), но не истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает какой-либо объект, и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, поэтому она применима только к суждениям, а не к понятиям.

4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом.

Как видим, суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части: субъект, предикат, связка и квантор.

Субъект (обозначается латинской буквой S) – это то, о чем идет речь в суждении. Например, в суждении Все учебники являются книгами речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники.

Предикат (обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении Все учебники являются книгами о субъекте (об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги.

Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является, это и т. п.

Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т. п.

Рассмотрим суждение Некоторые люди являются спортсменами. В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово являются, а слово некоторые представляет собой квантор. Если в каком-то суждении отсутствует связка или квантор, то они все равно подразумеваются. Например, в суждении Тигры – это хищники квантор отсутствует, но он подразумевается – это слово все. С помощью условных обозначений субъекта и предиката можно отбросить содержание суждения и оставить только его логическую форму. Например, если у суждения Все прямоугольники – это геометрические фигуры отбросить содержание и оставить форму то получится: Все S есть Р. Логическая форма суждения Некоторые животные не являются млекопитающими есть Некоторые S не есть Р.

Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие логические отношения: равнозначности, пересечения, подчинения и несовместимости.

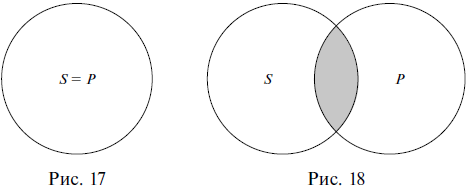
Отношение равнозначности предполагает, что субъект и предикат представляют собой равнозначные понятия. В суждении Все квадраты – это равносторонние прямоугольники субъект квадраты и предикат равносторонние прямоугольники находятся в отношении равнозначности, потому что квадрат – это обязательно равносторонний прямоугольник, а равносторонний прямоугольник – это обязательно квадрат (рис. 17).

Отношения равнозначности субъекта и предиката иллюстрируют примеры ниже:

Антарктида представляет собой ледовый материк (равнозначность).

Д. И. Менделеев – создатель Периодической системы химических элементов (равнозначность).

Отношение пересечения показывает, что субъект и предикат суждения являются пересекающимися понятиями. В суждении Некоторые писатели – это американцы субъект писатели и предикат американцы находятся в отношении пересечения (так как писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть) (рис. 18).

Отношением пересечения связаны субъект и предикат следующих суждений:

Некоторые русские писатели – это всемирно известные люди.

Некоторые грибы – несъедобные объекты.

Некоторые ученые – древние греки.

При отношении подчинения субъект и предикат суждения соотносятся как видовое и родовое понятия. В суждении Все тигры – это хищники субъект тигры и предикат хищники находятся в отношении подчинения, потому что тигр – это обязательно хищник, но хищник не обязательно тигр. Так же в суждении Некоторые хищники являются тиграми субъект хищники и предикат тигры находятся в отношении подчинения, будучи родовым и видовым понятиями.

Отношение подчинения хорошо иллюстрируют следующие суждения:

• Все бактерии являются живыми организмами.

• Солнце – это одна из звезд.

• Не все спортсмены являются олимпийскими чемпионами.

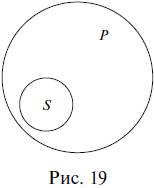
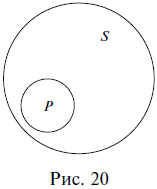
Отметим, в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объем субъекта полностью включается в объем предиката (рис. 19), или наоборот (рис. 20).

Отношение несовместимости означает, что субъект и предикат суждения являются несовместимыми (соподчиненными) понятиями. В суждении Все планеты не являются звездами субъект планеты и предикат звезды находятся в отношении несовместимости, так как ни одна планета не может быть звездой, и ни одна звезда не может быть планетой (рис. 21).

В приведенных ниже суждениях субъект и предикат находятся в отношении несовместимости:

Параллельные прямые не пересекаются (несовместимость).

Учебники не могут быть развлекательными книгами (несовместимость).

Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить, какое понятие данного суждения является субъектом, а какое предикатом. Для примера определим отношение между субъектом и предикатом в суждении Некоторые военнослужащие являются россиянами.

Сначала находим субъект суждения, – это понятие военнослужащие, затем устанавливаем его предикат, – это понятие россияне. Понятия военнослужащие и россияне находятся в отношении пересечения (военнослужащий может быть россиянином и может им не быть; и россиянин может как быть, так и не быть военнослужащим). Следовательно, в указанном суждении субъект и предикат пересекаются.

Точно так же в суждении Все планеты – это небесные тела субъект и предикат находятся в отношении подчинения, а в суждении Ни один кит не является рыбой субъект и предикат несовместимы.

Как правило, все суждения подразделяют на три вида:

Атрибутивные суждения (от лат. attributum – «неотъемлемый признак») – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение Все воробьи – это птицы – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта, ведь быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей).

Надо отметить, что в атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении Некоторые птицы – это воробьи (как видим, по сравнению с вышеприведенным примером, субъект и предикат поменялись местами) субъект является неотъемлемым признаком (атрибутом) предиката. Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта.

Экзистенциальные суждения (от лат. existentia – «существование») – это суждения, в которых предикат указывает на существование или несуществование субъекта. Например, суждение Вечных двигателей не бывает является экзистенциальным, так как его предикат не бывает свидетельствует о несуществовании субъекта (вернее – предмета, который обозначен субъектом).

Релятивные суждения (от лат. relativus – «относительный») – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение Москва основана раньше Санкт-Петербурга является релятивным, потому что его предикат основана раньше Санкт-Петербурга указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения.

В мышлении и языке большую часть составляют атрибутивные суждения. Они встречаются чаще, чем экзистенциальные и релятивные. Кроме того, последние, в принципе, можно представить как атрибутивные. Вернемся к экзистенциальному суждению Вечных двигателей не бывает. Его предикат (не быть или не существовать) вполне можно рассматривать как атрибут субъекта (вечные двигатели), ведь не существовать – это действительно неотъемлемый признак вечных двигателей, следовательно, данное суждение возможно расценивать как атрибутивное.

Теперь обратимся к релятивному суждению Москва основана раньше Санкт-Петербурга, предикат которого (быть основанным раньше Санкт-Петербурга) вполне можно рассматривать как атрибут субъекта (Москва), ведь быть старше Санкт-Петербурга (ранее основанным городом) – это действительно неотъемлемый признак Москвы. Таким образом, это суждение также возможно охарактеризовать как атрибутивное.

Все и некоторые, есть и не есть (Виды простых суждений)

Если в суждении присутствуют один субъект и один предикат, то оно является простым. Все простые суждения по объему субъекта и качеству связки делятся на четыре вида. Объем субъекта может быть общим (всё) и частным (некоторые), а связка может быть утвердительной (есть) и отрицательной (не есть).

На основе объема субъекта и качества связки можно выделить только четыре комбинации, которыми исчерпываются все виды простых суждений: все – есть, некоторые – есть, все – не есть, некоторые – не есть. Каждый из этих видов имеет свое название и условное обозначение.

Общеутвердительные суждения (обозначаются латинской буквой А) – это суждения с общим объемом субъекта и утвердительной связкой, т. е. одновременно общие и утвердительные: Все S есть Р. Например: Все школьники являются учащимися.

Частноутвердительные суждения (обозначаются латинской буквой I) – это суждения с частным объемом субъекта и утвердительной связкой, т. е. одновременно частные и утвердительные: Некоторые S есть Р. Например: Некоторые животные являются хищниками.

Общеотрицательные суждения (обозначаются латинской буквой Е) – это суждения с общим объемом субъекта и отрицательной связкой, т. е. одновременно общие и отрицательные: Все S не есть Р (или Ни одно S не есть Р). Например: Все планеты не являются звездами, Ни одна планета не является звездой.

Частноотрицательные суждения (обозначаются латинской буквой О) – это суждения с частным объемом субъекта и отрицательной связкой, т. е. одновременно частные и отрицательные: Некоторые S не есть Р. Например: Некоторые грибы не являются съедобными.

Далее следует ответить на вопрос, к каким суждениям – общим или частным – следует относить суждения с единичным объемом субъекта (т. е. те суждения, в которых субъект представляет собой единичное понятие), например: Солнце – это небесное тело, Москва основана в 1147 году, Антарктида – это один из материков Земли. Суждение является общим, если речь в нем идет обо всем объеме субъекта, и частным, если речь идет о части объема субъекта. В суждениях с единичным объемом субъекта речь идет обо всем объеме субъекта (в приведенных примерах – обо всем Солнце, обо всей Москве, обо всей Антарктиде). Таким образом, суждения, в которых субъект является единичным понятием, считаются общими (общеутвердительными или общеотрицательными). Так, три приведенных выше суждения – общеутвердительные, а суждение Известный итальянский ученый эпохи Возрождения Галилео Галилей не является автором теории электромагнитного поля – общеотрицательное.

В дальнейшем будем говорить о видах простых суждений, не употребляя их длинных названий, с помощью условных обозначений – латинских букв А, I, Е, О. Эти буквы, взятые из двух латинских слов: affirmo – «утверждать» и nego – «отрицать», были предложены в качестве обозначения видов простых суждений еще в Средние века.

Важно отметить, что в каждом из видов простых суждений субъект и предикат находятся в определенных отношениях. Так, общий объем субъекта и утвердительная связка суждений вида А приводят к тому, что в них субъект и предикат могут находиться в отношениях равнозначности или подчинения (других отношений между субъектом и предикатом в суждениях вида А быть не может). Например, в суждении Все квадраты (S) – это равносторонние прямоугольники (Р) субъект и предикат находятся в отношении равнозначности, а в суждении Все киты (S) – это млекопитающие животные (Р) – в отношении подчинения.

Частный объем субъекта и утвердительная связка суждений вида I обусловливают то, что в них субъект и предикат могут находиться в отношениях пересечения или подчинения (но не в других). Например, в суждении Некоторые спортсмены (S) – это негры (Р) субъект и предикат находятся в отношении пересечения, а в суждении Некоторые деревья (S) – это сосны (Р) – в отношении подчинения.

Общий объем субъекта и отрицательная связка суждений вида Е приводят к тому, что в них субъект и предикат находятся только в отношении несовместимости. Например, субъект и предикат несовместимы в суждениях Все киты (S) – это не рыбы (Р), Все планеты (S) не являются звездами (Р), Все треугольники (S) – это не квадраты (Р).

Частный объем субъекта и отрицательная связка суждений вида О обусловливают то, что в них субъект и предикат, так же как и в суждениях вида I, могут быть только в отношениях пересечения и подчинения. Например, в суждении Некоторые студенты (S) не являются спортсменами (Р) субъект и предикат находятся в отношении пересечения, а в суждении Некоторые геометрические фигуры (S) не являются треугольниками (Р) субъект и предикат находятся в отношении подчинения.

Обо всем или о части (Распределенность терминов в простых суждениях)

Терминами суждения называются его субъект и предикат.

Термин считается распределенным (развернутым, исчерпанным, взятым в полном объеме), если в суждении речь идет обо всех объектах, входящих в объем этого термина. Распределенный термин обозначается знаком «+», а на схемах Эйлера изображается полным кругом (кругом, который не содержит в себе другого круга и не пересекается с другим кругом) (рис. 22).

Термин считается нераспределенным (неразвернутым, неисчерпанным, взятым не в полном объеме), если в суждении речь идет не обо всех объектах, входящих в объем этого термина. Нераспределенный термин обозначается знаком «—», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг (рис. 23а) или пересекается с другим кругом (рис. 23б).

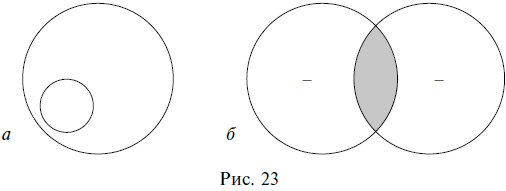
Например, в суждении Все акулы (S) являются хищниками (Р) речь идет обо всех акулах, значит, субъект этого суждения распределен. Однако в данном суждении речь идет не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределен. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределенному термину (субъекту акулы) соответствует полный круг, а нераспределенному (предикату хищники) – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть) (рис. 24).

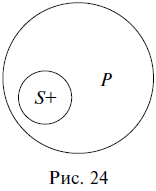
Распределенность терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом.

Проще всего устанавливать распределенность терминов в простых суждениях с помощью схем Эйлера. Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее еще проще – полный круг, как уже говорилось, соответствует распределенному термину, а неполный – нераспределенному. Например, требуется установить распределенность терминов в суждении Некоторые русские писатели – это всемирно известные люди. Сначала найдем в этом суждении субъект и предикат: русские писатели – субъект, всемирно известные люди – предикат. Теперь установим, в каком отношении они находятся. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идет речь в суждении (рис. 25).

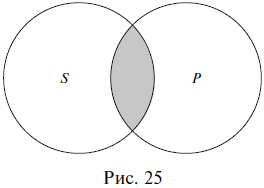
И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены (S —, Р —).

Рассмотрим еще один пример. Надо установить распределенность терминов в суждении Некоторые люди – это спортсмены. Найдя в этом суждении субъект и предикат (люди – субъект, спортсмены – предикат) и установив отношение между ними (подчинение), изобразим его на схеме Эйлера, заштриховав ту часть, о которой идет речь в суждении (рис. 26).

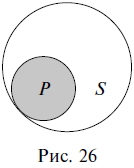
Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределен, а предикат распределен (S —, Р +).

Все не рыбы не являются карасями (Способы преобразования простых суждений)

Существует три способа преобразования, т. е. изменения формы, простых суждений: обращение, превращение и противопоставление предикату.

Обращение – это преобразование простого суждения, при котором субъект и предикат меняются местами. Например, суждение Все акулы являются рыбами преобразуется путем обращения в суждение Некоторые рыбы являются акулами. Здесь может возникнуть вопрос, почему исходное суждение начинается с квантора все, а новое – с квантора некоторые! Этот вопрос на первый взгляд кажется странным, ведь нельзя же сказать Все рыбы являются акулами, следовательно, единственное, что остается, это Некоторые рыбы являются акулами. Однако в данном случае мы обратились к содержанию суждения и по смыслу поменяли квантор все на квантор некоторые; а логика, как уже говорилось, отвлекается от содержания мышления и занимается только его формой. Поэтому обращение суждения Все акулы являются рыбами можно выполнить формально, не обращаясь к его содержанию (смыслу). Для этого установим распределенность терминов в этом суждении с помощью круговой схемы. Термины суждения, т. е. субъект акулы и предикат рыбы, находятся в данном случае в отношении подчинения (рис. 27).

На круговой схеме видно, что субъект распределен (полный круг), а предикат нераспределен (неполный круг). Вспомним, что термин распределен, когда речь идет обо всех входящих в него предметах, и нераспределен, когда – не обо всех, и автоматически мысленно поставим перед термином акулы квантор все, а перед термином рыбы – квантор некоторые. Делая обращение указанного суждения, т. е. меняя местами его субъект и предикат и начиная новое суждение с термина рыбы, мы опять же автоматически снабжаем его квантором некоторые, не задумываясь о содержании исходного и нового суждений, и получаем безошибочный вариант: Некоторые рыбы являются акулами.

Возможно, все это покажется чрезмерным усложнением элементарной операции, однако далее мы увидим,

Обратим внимание на то, что в рассмотренном выше примере исходное суждение было вида А, а новое – вида I, т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях Все акулы являются рыбами и Некоторые рыбы являются акулами речь идет об одном и том же. Суждение вида А обращается или само в себя, или в суждение вида I. Суждение вида I обращается или само в себя, или в суждение вида А. Суждение вида Е всегда обращается само в себя, а суждение вида О обращению не поддается.

Второй способ преобразования простых суждений, называемый превращением, заключается в том, что у суждения меняется связка: положительная на отрицательную, или наоборот. При этом предикат суждения заменяется противоречащим понятием (т. е. перед предикатом ставится частица НЕ). Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения Все акулы являются рыбами, преобразуется путем превращения в суждение Все акулы не являются не рыбами. Это суждение может показаться странным, ведь обычно так не говорят, хотя на самом деле перед нами более короткая формулировка той мысли, что ни одна акула не может быть таким существом, которое не является рыбой, или что множество всех акул исключается из множества всех существ, которые не являются рыбами. Субъект акулы и предикат не рыбы суждения, получившегося в результате превращения, находятся в отношении несовместимости (рис. 28).

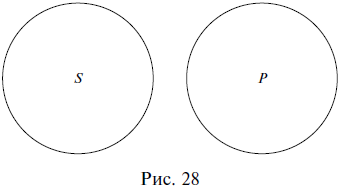
Приведенный пример превращения демонстрирует важную логическую закономерность: любое утверждение равно двойному отрицанию, и наоборот. Как видим, исходное суждение вида А в результате превращения стало суждением вида Е. В отличие от обращения превращение не зависит от характера отношений между субъектом и предикатом простого суждения. Поэтому суждение вида А всегда превращается в суждение вида Е, а суждение вида Е – в суждение вида А. Суждение вида I всегда превращается в суждение вида О, а суждение вида О – в суждение вида I.

Третий способ преобразования простых суждений – противопоставление предикату – состоит в том, что сначала суждение подвергается превращению, а потом обращению. Например, чтобы путем противопоставления предикату преобразовать суждение Все акулы являются рыбами, надо сначала подвергнуть его превращению. Получится: Все акулы не являются не рыбами. Теперь надо совершить обращение с получившимся суждением, т. е. поменять местами его субъект акулы и предикат не рыбы. Чтобы не ошибиться, вновь прибегнем к установлению распределенности терминов с помощью круговой схемы (субъект и предикат в этом суждении находятся в отношении несовместимости) (рис. 29).

На круговой схеме видно, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно, мы должны сопроводить как субъект, так и предикат квантором все. После этого совершим обращение с суждением Все акулы не являются не рыбами. Получится: Все не рыбы не являются акулами. Суждение звучит непривычно, однако это – более короткая формулировка той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе.

Все три операции преобразования простых суждений проще всего совершать с помощью круговых схем. Для этого надо изобразить кругами Эйлера три термина: субъект, предикат и понятие, противоречащее предикату (не-предикат). Потом следует установить их распределенность, и из получившейся схемы будут вытекать четыре суждения – одно исходное и три результата преобразований. Главное – помнить, что распределенный термин соответствует квантору все, а нераспределенный – квантору некоторые; что соприкасающиеся на схеме Эйлера круги соответствуют связке является, а несоприкасающиеся – связке не является. Например, требуется совершить три операции преобразования с суждением Все учебники являются книгами. Изобразим субъект учебники, предикат книги и не-предикат не книги круговой схемой и установим распределенность этих терминов (рис. 30).

Получившуюся круговую схему можно прочитать четырьмя способами:

• Все учебники являются книгами (исходное суждение).

• Некоторые книги являются учебниками (обращение).

• Все учебники не являются не книгами (превращение).

• Все не книги не являются учебниками (противопоставление предикату).

Рассмотрим еще один пример. Надо преобразовать тремя способами суждение Все планеты не являются звездами. Изобразим кругами Эйлера субъект планеты, предикат звезды и не-предикат не звезды. Обратите внимание на то, что понятия планеты и не звезды находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой, – это не обязательно планета. Установим распределенность этих терминов (рис. 31).

Получившуюся круговую схему можно прочитать четырьмя разными способами:

• Все планеты не являются звездами (исходное суждение).

• Все звезды не являются планетами (обращение).

• Все планеты являются не звездами (превращение).

• Некоторые не звезды являются планетами (противопоставление предикату).

Логический квадрат (Отношения между суждениями)

Простые суждения делятся на сравнимые и несравнимые.

Сравнимые (идентичные по материалу) суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику являются сравнимыми, так как у них совпадают субъекты и предикаты, а кванторы и связки различаются.

Несравнимые суждения имеют разные субъекты и предикаты. Например, суждения: Все школьники изучают математику, Некоторые спортсмены – это олимпийские чемпионы являются несравнимыми, так как субъекты и предикаты у них не совпадают.

Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.

Совместимыми называются суждения, которые могут быть одновременно истинными. Например, суждения Некоторые люди – это спортсмены, Некоторые люди – это не спортсмены являются одновременно истинными и представляют собой совместимые суждения.

Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).

Совместимые суждения могут находиться в отношениях равнозначности, подчинения или частичного совпадения.

Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения Москва является древним городом, Столица России является древним городом находятся в отношении равнозначности.

Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения Все растения являются живыми организмами, Все цветы (некоторые растения) являются живыми организмами находятся в отношении подчинения.

Частичное совпадение – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения Некоторые грибы являются съедобными и Некоторые грибы не являются съедобными находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные (I) и частноотрицательные (О).

Несовместимые суждения могут находиться в отношениях противоположности или противоречия.

Противоположность – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения Все люди являются правдивыми и Все люди не являются правдивыми находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные (Д) и общеотрицательные (Е).

Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Вернемся к приведенным выше суждениям и убедимся в этом: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми. Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями Все люди являются правдивыми и Все люди не являются правдивыми есть третий, средний вариант Некоторые люди являются правдивыми, а некоторые не являются таковыми, который, будучи истинным суждением, обусловливает одновременную ложность двух крайних противоположных суждений.

Противоречие – это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объемами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения Все люди являются правдивыми и Некоторые люди не являются правдивыми находятся в отношении противоречия.

Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот, ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы еще вернемся, когда речь пойдет о логических законах противоречия и исключенного третьего.

Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан еще средневековыми логиками.

Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия.

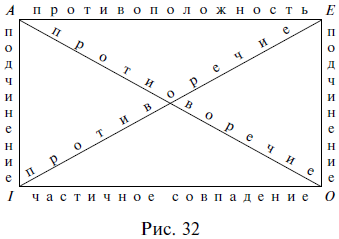
Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О.

Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – это противоречие.

Суждения Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.

Как уже говорилось, важным свойством суждений (в отличие от понятий) является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так, если суждение вида А является истинным или ложным, то три других (I, Е, О), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида А) тоже являются истинными или ложными.

Например, если суждение вида А: Все тигры – это хищники – истинно, то суждение вида I. Некоторые тигры – это хищники – также истинно (если все тигры – хищники, то и часть из них, т. е. некоторые тигры, – это тоже хищники); суждение вида Е Все тигры – это не хищники – ложно, и суждение вида О: Некоторые тигры – это не хищники – также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).

Чем дальше в лес, тем больше дров (Виды сложных суждений)

В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений: конъюнктивные, дизъюнктивные, импликативные, эквивалентные и отрицательные суждения.

Конъюнктивное суждение (конъюнкция) – это сложное суждение с соединительным союзом И, который обозначается в логике условным знаком «∧». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а ∧ b (читается «а и b»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: Сверкнула молния, и загремел гром является конъюнкцией (соединением) двух простых суждений: Сверкнула молния и Загремел гром. Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: Сверкнула молния, и загремел гром, и пошел дождь (а ∧ b ∧ с).

Дизъюнктивное суждение (дизъюнкция) – это сложное суждение с разделительным союзом ИЛИ. Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида: нестрогая и строгая дизъюнкция соответственно.

Нестрогая дизъюнкция – это сложное суждение с разделительным союзом ИЛИ в его нестрогом (неисключающем) значении, который обозначается знаком «∨». С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a ∨ b (читается «а или b»), где а и b – это два простых суждения. Например, сложное суждение Он изучает английский, или он изучает немецкий является нестрогой дизъюнкцией (разделением) двух простых суждений: Он изучает английский и Он изучает немецкий. Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.

Строгая дизъюнкция – это сложное суждение с разделительным союзом ИЛИ в его строгом (исключающем) значении, который обозначается знаком «∨_». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а ∨_ b (читается «или а, или b»), где а и b – это два простых суждения. Например, сложное суждение: Он учится в 9 классе, или он учится в 11 классе является строгой дизъюнкцией (разделением) двух простых суждений: Он учится в 9 классе, Он учится в 11 классе. Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.

Как нестрогая, так и строгая дизъюнкции могут состоять не только из двух, но и из большего числа простых суждений. Например: Он изучает английский, или он изучает немецкий, или он изучает французский (a ∨ b ∨ с); Он учится в 9 классе, или он учится в 10 классе, или он учится в 11 классе (a ∨_ b ∨_ c).

Импликативное суждение (импликация) – это сложное суждение с условным союзом ЕСЛИ…ТО, который обозначается знаком «=>». С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а => в (читается «если а, то b»), где а и b – это два простых суждения. Например, сложное суждение Если вещество является металлом, то оно электропроводно представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений: Вещество является металлом и Вещество электропроводно. В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом).

Первая часть импликации называется основанием, а вторая – следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: а => b, можно прочитать так: «если а, то обязательно b, но если b, то не обязательно а».

Эквивалентное суждение (эквиваленция) – это сложное суждение с союзом ЕСЛИ…ТО не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается знаком «<=>», с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а <=> b (читается «если а, то b, и если b, то а»), где а и b – это два простых суждения. Например, сложное суждение Если число является четным, то оно делится без остатка на 2 представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений: Число является четным и Число делится без остатка на 2. Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число четное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно четное.

Понятно, что в эквиваленции (в отличие от импликации) не может быть ни основания, ни следствия, так как две ее части являются равнозначными суждениями.

Отрицательное суждение (отрицание) – это сложное суждение с союзом НЕВЕРНО, ЧТО, который обозначается знаком «¬». С помощью этого знака отрицательное суждение можно представить в виде формулы: ¬ а (читается «неверно, что а»), где а – это простое суждение. Здесь может возникнуть вопрос: где же вторая часть сложного суждения, которую мы обычно обозначали символом b? В записи ¬ а, уже присутствуют два простых суждения: а – это какое-то утверждение, а знак «¬» – его отрицание. Перед нами как бы два простых суждения – одно утвердительное, другое отрицательное. Пример отрицательного суждения: Неверно, что все мухи являются птицами.

Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным пяти видам, и любое сложное суждение относится к одному из них. Например, сложное суждение Уж полночь близится, а Германна все нет является конъюнкцией, потому что в нем союз А употребляется в роли соединительного союза И. Сложное суждение Посеешь ветер, пожнешь бурю, в котором вообще нет союза, является импликацией, так как два простых суждения в нем связаны условным союзом ЕСЛИ…ТО.

Приведем еще несколько примеров сложных суждений с различными союзами естественного языка, которые выступают в роли нескольких рассмотренных нами логических союзов.

Живое существо является человеком только тогда, когда оно обладает мышлением (эквиваленция).

• Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны (нестрогая дизъюнкция).

• Вчера он получил двойку не только по математике, но еще и по русскому (конъюнкция).

• Проводник нагревается, когда через него проходит электрический ток (импликация).

• Окружающий нас мир либо познаваем, либо нет (строгая дизъюнкция).

• Либо же он совершенно бездарен, либо же полный лентяй (нестрогая дизъюнкция).

• Когда человек льстит, он лжет (импликация).

• Вода превращается в лед лишь при температуре от нуля градусов по Цельсию и ниже (эквиваленция).

Две прямые, лежащие в одной плоскости, не имеют общих точек только тогда, когда они параллельны (эквиваленция).

Вместо того, чтобы пойти в школу, он пошел гулять (конъюнкция).

Английский язык можно изучать либо в школе, либо на курсах, либо с репетитором, либо самостоятельно (нестрогая дизъюнкция).

То ли в мире действует всеобщая закономерность, то ли всеобщая случайность (строгая дизъюнкция).

Он не готовился к занятиям или систематически прогуливал их (нестрогая дизъюнкция).

Чем дальше в лес, тем больше дров (импликация).

Деревья качаются, потому что дует ветер (импликация).

Хотя на море разыгрался шторм, корабль неуклонно двигался своим курсом (конъюнкция).

• Глаза боятся, а руки делают (конъюнкция).

• Бели с утра шел дождь, то к полудню прояснилось (конъюнкция).

• Кончил дело, гуляй смело (импликация).

• Треугольник является равносторонним только тогда, когда все его углы равны (эквиваленция).

Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Ниже приведена таблица истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений. Таких наборов всего четыре:

• оба простых суждения истинные;

• первое суждение истинное, а второе ложное;

• первое суждение ложное, а второе истинное;

• оба суждения ложные.

Таблица

Как видим, конъюнкция (а ∧ b) истинна только тогда, когда истинны оба простых суждения, входящих в нее. Надо отметить, что конъюнкция, состоящая не из двух, а из большего количества простых суждений, также истинна только в том случае, когда истинны все входящие в нее суждения. Во всех остальных случаях она является ложной.

Нестрогая дизъюнкция (a ∨ b), наоборот, истинна во всех случаях за исключением того, когда оба входящих в нее простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, также ложна только тогда, когда ложны все входящие в нее простые суждения. Строгая дизъюнкция (а ∨_ b) истинна только тогда, когда одно входящее в нее простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, истинна только в том случае, если истинно только одно из входящих в нее простых суждений, а все остальные ложны.

Импликация (а => b) ложна только в одном случае, – когда ее основание является истинным, а следствие ложным. Во всех остальных случаях она истинна.

Эквиваленция (а <=> b) истинна тогда, когда два составляющих ее простых суждения истинны или же когда они оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна.

Проще всего определяется истинность отрицания: когда утверждение (а) истинно, его отрицание (¬ а) ложно; когда утверждение (а) ложно, его отрицание (¬ а) истинно.

Есть ли жизнь на Марсе? (Виды и правила вопросов)

Вопрос весьма близок к суждению. Это проявляется в том, что любое суждение можно рассматривать как ответ на некий вопрос. Поэтому вопрос – это логическая форма (конструкция), которая направлена на получение ответа в виде некоторого суждения.

Вопросы делятся на исследовательские и информационные.

Исследовательские вопросы направлены на получение нового знания. Это вопросы, на которые пока нет ответов, например: Как родилась Вселенная?

Информационные вопросы имеют своей целью приобретение (передачу от одного лица другому) уже имеющихся знаний (информации), например: Какова температура плавления свинца?

Вопросы также делятся на категориальные и пропозициональные.

Категориальные (восполняющие, специальные) вопросы включают в себя вопросительные слова кто, что, где, когда, почему, как и т. п., указывающие направление поиска ответов и, соответственно, категорию объектов, свойств или явлений, в которой следует искать нужные ответы. Категориальным, например, является вопрос Кто создал Периодическую систему химических элементов?

Пропозициональные (уточняющие, общие) вопросы направлены на подтверждение или отрицание некоей уже имеющейся информации. В этих вопросах ответ как бы уже заложен в виде готового суждения, которое надо лишь подтвердить или отвергнуть. Вопрос Полезно ли изучение математики? является пропозициональным.

Понятно, что и исследовательские, и информационные вопросы могут быть как категориальными, так и пропозициональными. Например: Как создать универсальное доказательство теоремы Ферма? – исследовательский категориальный вопрос; Есть ли во Вселенной планеты, населенные, как и Земля, разумными существами? – исследовательский пропозициональный вопрос; Когда появилась логика? – информационный категориальный вопрос; Верно ли, что число π – это отношение длины окружности к ее диаметру? – информационный пропозициональный вопрос.

Приведем еще несколько примеров вопросов.

• Когда был открыт закон Всемирного тяготения? (информационный категориальный вопрос).

• Смогут ли жители Земли расселиться на других планетах Солнечной системы? (исследовательский пропозициональный вопрос).

• В каком году родился Наполеон? (информационный категориальный вопрос).

• Каково будущее человечества? (исследовательский категориальный вопрос).

• Возможно ли предотвратить третью мировую войну? (исследовательский пропозициональный вопрос).

• Что такое тригонометрия? (информационный категориальный вопрос).

• Можно ли измерить расстояние от Земли до Луны? (информационный пропозициональный вопрос).

• Кто является создателем квантовой теории? (информационный категориальный вопрос).

• Чем отличаются естественные науки от гуманитарных? (информационный категориальный вопрос).

• Вел ли Древний Рим продолжительные завоевательные войны? (информационный пропозициональный вопрос).

• В чем смысл человеческой жизни? (исследовательский категориальный вопрос).

• Где находится самое высокое место земного шара? (информационный категориальный вопрос).

• Чему равна скорость света? (информационный категориальный вопрос).

• Что такое любовь? (исследовательский категориальный вопрос).

• Верно ли, что геоцентрическая картина мира появилась еще в древности? (информационный пропозициональный вопрос).

• Как зародилась жизнь во Вселенной? (исследовательский категориальный вопрос).

Достигнут ли люди когда-нибудь всеобщего процветания? (исследовательский пропозициональный вопрос).

• Как доказывается теорема Пифагора? (информационный категориальный вопрос).

• Возможно ли полное преодоление социальной несправедливости? (исследовательский пропозициональный вопрос).

• Кто считается создателем формальной логики? (информационный категориальный вопрос).

Любой вопрос имеет определенную структуру и состоит из двух частей. Первая часть представляет собой некую информацию (выраженную, как правило, каким-нибудь суждением), а вторая часть указывает на ее недостаточность и необходимость ее дополнения каким-либо ответом. Первая часть, называется основной (базисной) (ее также иногда называют предпосылкой вопроса), а вторая часть – искомой. Например, в информационном категориальном вопросе Когда была создана теория электромагнитного поля? основная часть – это утвердительное суждение Была создана теория электромагнитного поля, а искомая часть, представленная вопросительным словом когда, указывает на недостаточность информации, содержащейся в базисной части вопроса, и требует ее дополнения, которое следует искать в области (категории) временных явлений.

В исследовательском пропозициональном вопросе Возможны ли полеты землян в другие галактики? основная часть представлена суждением Возможны полеты землян в другие галактики, а искомая часть, выраженная частицей ли, указывает на необходимость подтверждения или отрицания этого суждения. В данном случае искомая часть вопроса свидетельствует не об отсутствии какой-то информации, содержащейся в его базисной части, а об отсутствии знания о ее истинности или ложности и требует это знание получить.

Наиболее важное логическое требование к постановке вопроса заключается в том, чтобы его базисная часть была истинным суждением. В этом случае вопрос считается логически корректным. Если же основная часть вопроса представляет собой ложное суждение, то вопрос следует признать логически некорректным (подобные вопросы не требуют ответа и подлежат отвержению).

Например, вопрос Когда было предпринято первое кругосветное путешествие? является логически корректным, поскольку его основная часть выражена истинным суждением В истории человечества имело место первое кругосветное путешествие. Вопрос В каком году знаменитый английский ученый Исаак Ньютон закончил работу над общей теорией относительности? логически некорректен, так как его основная часть представлена ложным суждением Автором общей теории относительности является знаменитый английский ученый Исаак Ньютон.

Итак, основная (базисная) часть вопроса должна быть истинной и не должна быть ложной. Однако существуют логически корректные вопросы, основные части которых являются ложными суждениями. Например, вопросы Возможно ли создание вечного двигателя? Есть ли разумная жизнь на Марсе? Изобретут ли машину времени? несомненно, следует признать логически корректными, несмотря на то, что их базисные части представляют собой ложные суждения: Возможно создание вечного двигателя, Есть разумная жизнь на Марсе, Изобретут машину времени. Дело в том, что искомые части этих вопросов направлены на выяснение истинностных значений их базисных частей, т. е. требуется выяснить, истинными или ложными являются суждения Возможно создание вечного двигателя, Есть разумная жизнь на Марсе, Изобретут машину времени. В этом случае вопросы логически корректны. Если бы искомые части рассматриваемых вопросов не были направлены на выяснение истинности их основных частей, а имели бы своей целью нечто иное, эти вопросы являлись бы логически некорректными, например: Где был создан первый вечный двигатель? Когда появилась разумная жизнь на Марсе? Сколько будет стоить путешествие на машине времени?

Таким образом, главное правило постановки вопроса следует расширить и уточнить: основная (базисная) часть корректного вопроса должна быть истинным суждением. Если же она является ложным суждением, то его искомая часть должна быть направлена на выяснение истинностного значения основной части; в противном случае вопрос будет логически некорректным.

Нетрудно догадаться, что требование для основной части быть истинной, по преимуществу, относится к категориальным вопросам, а требование того, чтобы искомая часть была выяснением истинности основной части, относится к пропозициональным вопросам.

Надо отметить, что корректные категориальные и пропозициональные вопросы сходны между собой в том, что на них всегда можно дать истинный ответ (как, впрочем, и ложный). Например, на категориальный вопрос Когда закончилась Первая мировая война? можно дать как истинный ответ (В 1918 году), так и ложный (В 1916 году). На пропозициональный вопрос Вращается ли Земля вокруг Солнца? также можно дать как истинный ответ (Да, вращается), так и ложный (Нет, не вращается). Отметим, что оба приведенных вопроса логически корректны.

Итак, принципиальная возможность получения истинных ответов есть основной признак корректных вопросов. Если же получить истинные ответы на некие вопросы принципиально невозможно, то они являются некорректными.

Например, нельзя получить истинный ответ на пропозициональный вопрос Закончится ли когда-нибудь Первая мировая война? так же, как невозможно получить его на категориальный вопрос С какой скоростью вращается Солнце вокруг неподвижной Земли? Любые ответы на эти вопросы необходимо будет признать неудовлетворительными, а сами вопросы – логически некорректными, подлежащими отвержению.

Умозаключение

Сделаем вывод (Что такое умозаключение)

Умозаключение – это форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением (выводом). Например:

Все живые организмы питаются влагой.

Все растения – это живые организмы.

=> Все растения питаются влагой.

В приведенном примере первые два суждения являются посылками, а третье – выводом. Посылки должны быть истинными суждениями и должны быть связаны между собой. Если хотя бы одна из посылок ложна, то и вывод ложен:

Все птицы – это млекопитающие животные.

Все воробьи – это птицы.

=> Все воробьи – это млекопитающие животные.

Как видим, в приведенном примере ложность первой посылки приводит к ложному выводу, несмотря на то что вторая посылка является истинной. Если посылки между собой не связаны, то вывод из них сделать невозможно. Например, из следующих двух посылок никакого вывода не следует:

Все планеты – это небесные тела.

Все сосны являются деревьями.

=>?

Обратим внимание на то, что умозаключения состоят из суждений, а суждения – из понятий, т. е. одна форма мышления входит в другую в качестве составной части.

Все умозаключения делятся на непосредственные и опосредованные.

В непосредственных умозаключениях вывод делается из одной посылки. Например:

Все цветы являются растениями.

=> Некоторые растения являются цветами.

Верно, что все цветы являются растениями.

=> Неверно, что некоторые цветы не являются растениями.

Нетрудно догадаться, что непосредственные умозаключения представляют собой уже известные нам операции преобразования простых суждений и выводы об истинности простых суждений по логическому квадрату. Первый приведенный пример непосредственного умозаключения является преобразованием простого суждения путем обращения, а во втором примере по логическому квадрату из истинности суждения вида А делается вывод о ложности суждения вида О.

В опосредованных умозаключениях вывод делается из нескольких посылок. Например:

Все рыбы – это живые существа.

Все караси – это рыбы.

=> Все караси – это живые существа.

Опосредованные умозаключения делятся на три вида: дедуктивные, индуктивные и умозаключения по аналогии.

Дедуктивные умозаключения (дедукция) (от лат. deductio – «выведение») – это умозаключения, в которых из общего правила делается вывод для частного случая (из общего правила выводится частный случай). Например:

Все звезды излучают энергию.

Солнце – это звезда.

=> Солнце излучает энергию.

Как видим, первая посылка представляет собой общее правило, из которого (при помощи второй посылки) вытекает частный случай в виде вывода: если все звезды излучают энергию, значит, Солнце тоже ее излучает, потому что оно является звездой.

В дедукции рассуждение идет от общего к частному, от большего к меньшему, знание сужается, в силу чего дедуктивные выводы достоверны, т. е. точны, обязательны, необходимы. Посмотрим еще раз на приведенный пример. Мог бы из двух данных посылок вытекать иной вывод, кроме того, который из них вытекает? Не мог. Вытекающий вывод – единственно возможный в этом случае. Изобразим отношения между понятиями, из которых состояло наше умозаключение, кругами Эйлера. Объемы трех понятий: звезды (3); тела, излучающие энергию (Т) и Солнце (С) схематично расположатся следующим образом (рис. 33).

Если объем понятия звезды включается в объем понятия тела, излучающие энергию, а объем понятия Солнце включается в объем понятия звезды, то объем понятия Солнце автоматически включается в объем понятия тела, излучающие энергию, в силу чего дедуктивный вывод и является достоверным.

Несомненное достоинство дедукции заключается в достоверности ее выводов. Вспомним, известный литературный герой Шерлок Холмс пользовался дедуктивным методом при раскрытии преступлений. Это значит, что он строил свои рассуждения таким образом, чтобы из общего выводить частное. В одном произведении, объясняя доктору Ватсону сущность своего дедуктивного метода, он приводит такой пример. Около убитого полковника Эшби сыщики Скотланд-Ярда обнаружили выкуренную сигару и решили, что полковник выкурил ее перед смертью. Однако Шерлок Холмс неопровержимо доказывает, что полковник не мог выкурить эту сигару, потому что он носил большие, пышные усы, а сигара выкурена до конца, т. е., если бы ее курил полковник Эшби, то он непременно подпалил бы свои усы. Следовательно, сигару выкурил другой человек.

В этом рассуждении вывод выглядит убедительно именно потому, что он дедуктивный – из общего правила: Любой человек с большими, пышными усами не может выкурить сигару до конца, выводится частный случай: Полковник Эшби не мог выкурить сигару до конца, потому что носил такие усы. Приведем рассмотренное рассуждение к принятой в логике стандартной форме записи умозаключений в виде посылок и вывода:

Любой человек с большими, пышными усами не может выкурить сигару до конца.

Полковник Эшби носил большие, пышные усы.

=> Полковник Эшби не мог выкурить сигару до конца.

Индуктивные умозаключения (индукция) (от лат. inductio – «наведение») – это умозаключения, в которых из нескольких частных случаев выводится общее правило. Например:

Юпитер движется.

Марс движется.

Венера движется.

Юпитер, Марс, Венера – это планеты.

=> Все планеты движутся.

Первые три посылки представляют собой частные случаи, четвертая посылка подводит их под один класс объектов, объединяет их, а в выводе говорится обо всех объектах этого класса, т. е. формулируется некое общее правило (вытекающее из трех частных случаев).

Легко увидеть, что индуктивные умозаключения строятся по принципу, противоположному построению дедуктивных умозаключений. В индукции рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы (в отличие от дедуктивных) не достоверны, а вероятностны. В рассмотренном выше примере индукции признак, обнаруженный у некоторых объектов какой-то группы, перенесен на все объекты этой группы, сделано обобщение, которое почти всегда чревато ошибкой: вполне возможно наличие в группе каких-то исключений, и даже если множество объектов из некоторой группы характеризуется каким-то признаком, то это не означает, что таким признаком характеризуются все объекты данной группы. Вероятностный характер выводов является, конечно же, недостатком индукции. Однако ее несомненное достоинство и выгодное отличие от дедукции, которая представляет собой сужающееся знание, заключается в том, что индукция – это расширяющееся знание, способное приводить к новому, в то время как дедукция – это разбор старого и уже известного.

Умозаключения по аналогии (аналогия) (от греч. analogia – «соответствие») – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь.

Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода.

=> Вероятно, на Марсе есть жизнь.

Как видим, сопоставляются два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в Солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.

Когда все суждения простые (Категорический силлогизм)

Все дедуктивные умозаключения называются силлогизмами (от греч. sillogismos – «подсчитывание, подытоживание, выведение следствия»). Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все входящие в него суждения (две посылки и вывод) являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.

Рассмотрим пример простого силлогизма:

Все цветы (М) – это растения (Р).

Все розы (S) – это цветы (М).

=> Все розы (S) – это растения (Р).

Обе посылки и вывод являются в данном силлогизме простыми суждениями, причем и посылки, и вывод – это суждения вида А (общеутвердительные). Обратим внимание на вывод, представленный суждением Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Так же в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы можно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).

В файле поместилась только часть книги.